Conceptual misunderstanding of impulses

Question

This is a 1998 IPHO Mechanics problem analyzing a rolling hexagonal prism (a pencil). A similar question was asked on PSE but the question is unanswered and nobody gave a proper explanation but just a link to the answer solution.

You can solve this question by conserving angular momentum about the vertex that hit the plane, i.e angular momentum about that point during the brief instant is conserved. But an alternative solution was also given in the answer key which doesn't make much sense to me. It said after impact there is an impulse perpendicular to the plane which makes sense but also apparently there is an impulse parallel to and up the incline, which i don't understand why. And the way they set up the equations isn't that clear. All I can understand is that there is a normal impulse from the ground because at the point of collision velocity of the vertex was perpendicular to the incline and since the vertex is at rest after impact there was an impulse, but why horizontal impulse?

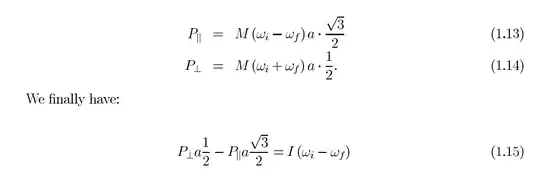
How were the equations set up?

Answer 1

The component of the impulse parallel to the plane is provided by the frictional force, while the component perpendicular to the plane is provided by the normal reaction from the new point of pivot. Impulse momentum theorem has been used, taking the respective components of momenta. Note that the velocities have been found using the relation $$ \vec{v} = \vec{\omega} \times \vec{r} $$

For the final equation, It is simply using the definition of angular impulse, as it is equal to the change in angular momentum, about the center of mass. The torques due to the impulses are taken into account, about the center of mass.

Please keep in mind the sign convention used here, up the incline has been taken as negative, and the direction for torques favoring rotation has been taken as positive. (You could set your own sign convention, just be consistent with it)

Hope you got it