Perhaps it might help to consider how sound is heard, and how it can be mechanically recorded a vinyl record.
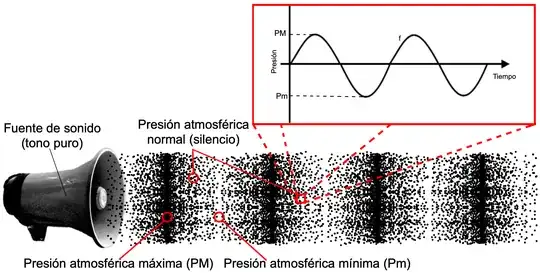
Sound is just the change of air pressure, measured at a point.
So, we hear by the diaphragm of our eardrum mechanically displacing in and out, pushed and pulled by soundwaves. This displacement is one-dimensional, like any drum-skin: in or out. How fast it wiggles in or out is the pitch. How far it wiggles in or out is the volume. But at any moment in time, our eardrum is only in one position, with a certain displacement from its rest position.
To record it mechanically on a vinyl record, we take the vibrations of a similar mechanical diaphragm, and connect it to a needle, which scratches a surface in a way that exactly reproduces those vibrations. Like a heart monitor or a seismograph, but for sound waves.
Only one wiggly line scratched into a surface stores all frequencies and amplitudes (pitches and volumes) of the sound. Well, OK, it can get a bit cleverer for stereo, but let's ignore that for now!
There isn't one line for each frequency: there's just one single wavy line, or "waveform". For any point in time, all that line has "stored" for all of the sounds in a musical recording, is the diaphragm's displacement from the rest position.
Just as with our eardrums, the displacement doesn't contain any information about frequency, or about what instrument was playing, or anything. Just "how loud that sound was, right then."
But the changing values of that one displacement value over time is how all the subtlety and nuance of a myriad different sounds in a music track are heard. All the instruments and singing, all stored in that one wavy line.
Are we exactly reproducing the sound, as it truly was? No, there will be elements of the sound that are too high-frequency to move the diaphragm, since the diaphragm has mass. But long as the diaphragm-and-needle combination is at least as sensitive to air movement as the diaphragm of the human eardrum, though, it'll reproduce enough of the sound to replay the whole spectrum of audible sound.
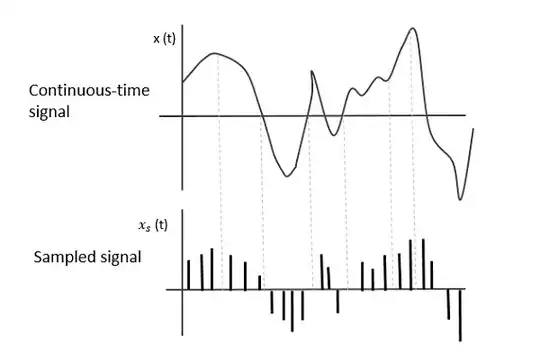
So, what if we want to store that wiggly wave as a sequence of discrete numbers?
We'd slice that wiggly line up into parts and write down the displacement at each point.
If we do it often enough, we should be able to send those values to control a speaker diaphragm to move forward and backwards by the amounts we'd recorded, and it'll move in the same path as the scratched line we recorded earlier.
How big should the numbers be, that we use to write down the displacement? Well, if we figure out the smallest change in displacement our recording equipment (or our ears) can detect, that should be the value of '1' our recording. Doesn't necessarily even need to be linear: maybe our ears don't respond linearly to changes in volume, in which case the volume difference between "0" and "1" can be different to that between "500" and "501".
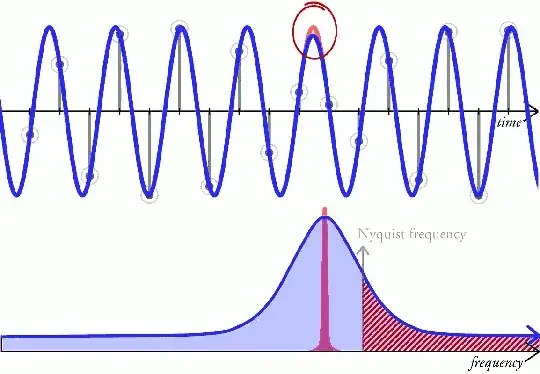
How often should we write the numbers down? Well, there's no point recording/sampling more often than the fastest the diaphragm (or our ears) can move between two adjacent numbers, since the values can't change more often than that.