Are Maxwell's equations ideal approximations?

Question

So, I'm revising Maxwell's equations to understand how they work a little better, but Faraday's law seemed a little tricky to me for some reasons, so I came to the conclusion that Maxwell's equations must be approximations to physical phenomena from ideal situations.

To understand what I'm talking about, let’s imagine a charged particle traveling perpendicular to a constant uniform magnetic field, at a constant speed, without any parallel velocity component. The Lorentz's force equation predicts that this particle will move along a sufficiently small circle:

$$F_L=q(\vec{E}+\vec{v}\times\vec{B})$$

According to M.E.:

$$\nabla\times\vec{E}=-\frac{\partial\vec{B}}{\partial t}$$

Now, since the magnetic field is constant, $\frac{\partial\vec{B}}{\partial t}=0$, so

$$F_L=q(\vec{v}\times\vec{B})$$

This reasoning is backed up by the behaviour of electromagnetic phenomena we encounter in experiments, but is the electric field really zero? Doesn't the charged particle generate an non-zero electric field that itself affects the magnetic field, affecting the particle?

I believe we haven't yet developed the mathematical tools to deal with these kind of self-interactions, so the only thing that seems plausible is to neglect the contribution of the charged particle to the magnetic field, because it’s some orders of magnitude smaller. What can you say about this?

Answer 1

Maxwell's equations are purely classical. They do not account for quantum effects, so they do not explain non-classical phenomena such as photon-photon scattering, the photoelectric effect or Planck's law. They are also based on the empirical premise that there are no magnetic monopoles, so if evidence for magnetic monopoles were ever found, then Maxwell's equations would have to be modified.

Having said that, Maxwell's equations are the classical limit of quantum electrodynamics, which is possibly the most exhaustively tested theory in the whole of physics. So if there is a non-quantum scenario which Maxwell's equations do not describe accurately, then we have not come across it yet.

However, we do know that the Lorentz force (which is not part of Maxwell's equations) is an approximation. The Lorentz force formula is corrected and generalised by the Abraham-Lorentz force.

Answer 2

From the classical point of view, the self-interaction of a charged particle mediated by the electromagnetic field is a problematic topic. The reason is not in some inadequacy of Maxwell's equations. As far as we know, they describe all the existing phenomenology at the classical level and provide a firm basis for quantizing the electromagnetic field, giving us an extremely accurate theory even at the quantum level.

The problematic side is the dynamics of the charged particle.

On the classical side, we have to remember that the splitting of the interactions into multiplication of a factor depending on particle properties (charge, current) and a field (${\bf E}$ or ${\bf B}$) determined by some external source, but not from the particle, is consistent with the classical way of conceptually introducing fields: from an effective decoupling based on the idea that we can make the effect of the particle on the field as smallest as possible. Think, for example, the case of the electric field. The conceptual definition can be formally written as $$ {\bf E} = \lim_{q \rightarrow 0} \frac{\bf F}{q}, $$ where $q$ is the charge on an electrified body, and ${\bf F}$ the electric force acting on it. The limit is required precisely to avoid the perturbation of the field induced by the body, which would modify the force, requiring a self-consistent treatment. While taking into account such self-consistency is easy in the static case, the dynamic case is extremely more complicated. The main reason is the dependence of the total field (due to external charges and currents and to the charged particle) on the retarded position and velocity of the particle itself.

We need perturbative solutions when we need to consider such self-interaction effects. Usually, the accuracy required at the microscopic level is much higher than at the macroscopic level. This fact explains what perturbative methods have been explored much more deeply in the quantum description of particle dynamics. There, the best description level we have is Quantum Electrodynamics. A whole set of perturbative techniques, including renormalization, have been developed to deal with the self-consistent description of the dynamics of a particle and electromagnetic fields.

Answer 3

First, if $\vec{\nabla}\times\vec{E}=0$, it does not mean that $\vec{E}=0$. However, you are right, the equations you use require corrections (even if we don't take quantum physics into account). The charged particle in a magnetic field moves with a centripetal acceleration, so it radiates electromagnetic radiation (synchrotron radiation) and thus loses energy. Thus, there is indeed backreaction of a charged particle, and one needs a correction to the Lorentz force, which correction is Abraham-Lorentz-Dirac force (see, e.g., https://web.physics.ucsb.edu/~davidgrabovsky/files-notes/Self-Force.pdf).

Answer 4

I am going to reply a bit off topic here in that I am going to argue that Maxwell's equations, as they are commonly presented in modern texts, do not cover all possible situations of field generation. And that is even without considering the thorny issue of self-interactions mentioned by the OP and which have been covered to some extent by other answers.

The set of equations I am talking about are

\begin{eqnarray} & & \vec{\nabla}\cdot \vec{E}=\frac{\rho}{\varepsilon_0} \\ & & \vec{\nabla}\cdot \vec{B}=0 \\ & & \vec{\nabla} \times \vec{E} = -\frac{\partial \vec{B}}{\partial t} \\ & & \vec{\nabla}\times \vec{B} = \mu_0 \vec{j} + \frac{1}{c^2}\frac{\partial \vec{E}}{\partial t} \end{eqnarray}

Now, the 3rd Maxwell equation written above is supposed to be a PDE capturing Faraday's law. What this means is that, in principle, whether one wants to solve a problem of field generation involving Faraday's law, it should be equivalent to solve it using the 'macroscopic' law equating the induced $emf$ in a circuit to the (negative of the) time variation of the magnetic flux across a conducting loop or by solving the PDE given by the 3rd Maxwell equation written above.

Now, I am pretty sure that you have heard of the Laplace rails. They consist in a rectangular conducting loop with one of the sides that is actually mobile. When immersed in a uniform and constant magnetic field, moving the mobile part at some constant velocity $\vec{v}$ generates an $emf$ (and a corresponding non-potential electric field) in the conducting loop. See figure below taken from Ref 1.

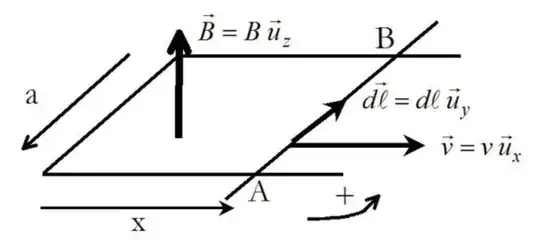
As far as I am aware, explaining the generation of this $emf$ and corresponding non-potential electric field is not possible (unless someone comes up with a very contrived model-dependent solution) with the 3rd Maxwell equation provided above.

The reason for this is that in the derivation of the 3rd Maxwell equation from the macroscopic equation

\begin{eqnarray} && \oint_{\partial \Omega} \vec{E}\cdot \vec{d\ell} =-\frac{d}{dt} \iint_{\Omega} \vec{B}\cdot \vec{dS}, \end{eqnarray}

one often omits the fact that it is assumed that the domain $\Omega$ over which the flux is calculated actually may depend on time.

Consequently, a true 'microscopic' Maxwell PDE equation capturing fully Faraday's law of induction should in principle account for the kinematics of $\Omega(t)$ which is quite complicated to capture in all generality.

However, in cases of moving rigid bodies like for Laplace rails described above, one can find that the 3rd Maxwell equation needs to be amended in the following manner

\begin{equation} \vec{\nabla} \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}+ \vec{\nabla} \times \left(\vec{v} \times \vec{B} \right) \end{equation}

I could not find such descriptions in most common reference texts in electromagnetism and I certainly was not told about it during my studies.

The only treatments I am aware of are from The Classical Theory of Electricity and Magnetism by Abraham and Becker (page 141) and a slightly more model-dependent one in Classical Electricity and Magnetism by W.K.H. Panofsky (page 147).

It is noteworthy that the above modified equation is mentioned for moving media in Jackson's famous textbook on Classical Electrodynamics but the author claims that one can just do away with the $\vec{\nabla}\times(\vec{v}\times \vec{B})$ term by putting oneself in a proper inertial frame. I am not too sure this argument holds in all cases, especially when the field across a closed loop is concerned.