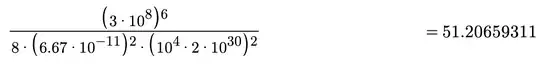Closest possible flyby to a nonrotating supermassive black hole

Question

Imagine you think Laplace is the last word on black holes. That is, you are aware of the radius for which the escape velocity is $c$, but you think gravity is Newtonian. You set your spacecraft on a course meant to be a hyperbola that remains just outside the event horizon of a giant, nonrotating black hole. Tidal forces are not a problem, and your plan is simply to observe conditions near the boundary.

Unfortunately, gravity is not Newtonian, and once you get inside the photon sphere you will need to exert thrust to get back out. (I originally thought the ISCO was the key boundary here, but it's not.) The closer you get to the black hole, the more thrust you will need. My sense is that, even when tidal forces are too small to be a concern, there is a closest distance that any object made of matter can get to the event horizon and later return to infinity without being crushed by the acceleration it would have to undergo to escape the photon sphere.

What I would really like is a number, something like the closest you can get to the event horizon and then escape without any object larger than a meter in height being reduced to degenerate matter. But that is still too vague to answer. So instead, is there a formula for the peak thrust you need to return to infinity as a function of the minimum number of Schwarzschild radii from the center?

Answer 1

OP asked: is there a formula for the peak thrust you need to return to infinity as a function of the minimum number of Schwarzschild radii from the center?

Yes, you can find the working here. The amount of force required to radially espace a Schwarzschild black hole of mass $M$ is $$F=m a=\frac{G M m}{r^{2}} \frac{1}{\sqrt{1-\frac{2 G M}{c^{2} r}}}.$$

OP asked: What is the closest you can get to the event horizon and then escape without any object larger than a meter in height being reduced to degenerate matter.

Assuming that your object only extends in the radial direction with length $\chi$, the tidal force acting on this object can be calculated using the equation of geodesic deviation. In the freely falling observer's frame this will give you $$ \frac{d^{2} \chi^r}{d \tau^{2}}=-R_{{c} {b} {c}}^{{r}} \chi^{{b}}$$ which on substituting the appropriate values of the Riemann tensor ${R^a}_{bcd}$ will give $$ \frac{d^{2} \chi^{{r}}}{d \tau^{2}}= \frac{2GM}{r^{3}} \chi^{{r}}.$$

So, the tidal force depends on the radial value $r$. Let us say we want to find out the tidal force at the event horizon ($r_{\rm hor} = 2GM/c^2$) of this black hole. Then $$ \frac{d^{2} \chi^{{r}}}{d \tau^{2}}= \frac{c^6}{8 G^2 M^2} \chi^{{r}}.$$ So we find that the larger the $M$, the smaller the tidal force at the horizon becomes. On doing some calculation, I find that for $M = 10^4 M_{\odot}$ the tidal force is $51$ N (see pic below)