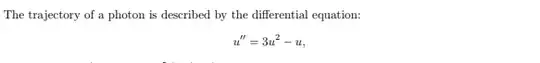-1

I am currently working on some work with neutron stars so this led me to calculations of photon trajectories in curved spacetime.

enter image description here

These are the steps I followed to write code that would produce cartesian coordinates for me to graph.

enter image description here

I utilized this equation to form the steps listed above.

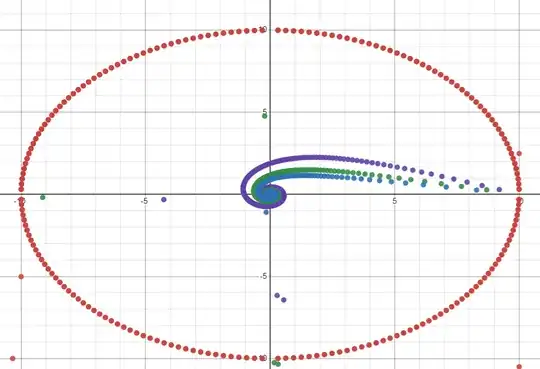
enter image description here

This is the graph of various trajectories when the photon is initialized at phi=0. In these scenarios the only variable adjusted is initial direction of photon motion(alpha). When alpha=pi/2 I get this circular trajectory. When alpha=pi/3, pi/4, and so on, I get the rotating spiral path which appears to be correct. Why is it that the graph is circular? Is this incorrect physically? It is important to note that I used polar coordinates in my calculations then converted back to cartesian.

Qmechanic
  • 220,844
kkrish
  • 1

1 Answers1

1

I think your result is correct: for $ \phi_0=0 $, if $ \alpha_0={\pi\over 2} $ the path is circular.

This is due to the fact that the equation $ u''=3u^2-u $ can be integrated if you multiply it by $ 2u' $, that is

$ 2u'u''=6u'u^2-2u'u $ which gives the integration

$ u'^2=2u^3-u^2+cte\ \ \ \ [1] $

If $ \phi_0=0 $ and $ \alpha_0={\pi\over 2} $, you have $ u'_0=0 $ (because $ \tan\phi_0=0 $ and $ \tan\alpha_0=\infty $).

This means $ u_1=u_0 $ and $ [1] $ leads to $ u'_1=u'_0 $ which is $ 0 $.

So, you will see that $ \forall n\ u'_n=0 $ and $ u_n=u_0 $ which results in a circular trajectory.

Hoping to have answered your question,

Best regards.

Cornelius Fyla
  • 191