Idk where, but at some point i heared the Event Horizons of a Schwarzschild black hole and Darkstar coincidentally are the same size. I have since then done a lot of stuff in GR, including Kerr black holes and wanted to revisit the Darkstar. I found the Event Horizon to actually equal $r_d = \frac{GM}{c}$
Which is of course half of a Schwarzschild Black Hole, being $r_s = \frac{2GM}{c^2}$ if memory serves me correctly. It is of course possible my "derivation" for the Darkstar is just wrong. In Cartesian coordinates my photon direction equation is;
$$\overrightarrow{d} = ||\overrightarrow{rayDir}+\left(\frac{||\overrightarrow{rayOrig}||\frac{GM}{r^2}h}{c}\right)||$$
Before yall get the pitchforks out, yes i am mixing vectors and numbers, i am not great at math. I have tried to take this equation into its component form, but it didnt work, i did something wrong.
I should note, $h$ is the step size, while $\overrightarrow{rayDir}$ is the normalized direction and $\overrightarrow{rayOrig}$ the ray position vector, both in cartesian coordinates.
My derivation, if you can call it that, is really more logic based than anything. The basic idea is to calculate the "Momentum" of our photon which is done with $\frac{||\overrightarrow{rayOrig}||\frac{GM}{r^2}h}{c}$. Momentum is direction * magnitude, so since the BH is at 0,0,0 the direction is just the current normalized position, or $||\overrightarrow{rayOrig}||$. The magnitude is the gravitational potential, $\frac{GM}{r^2}$, factored with the temporal step $h$. The $\frac{x}{c}$ bit is probably the most ad hoc aspect because my justification for it is that it checks out. If the speed of light is say double, the Horizon is half as big.
The whole party is updated as such;
$\overrightarrow{rayDir} = \overrightarrow{d}$
$\overrightarrow{rayOrig} += \overrightarrow{d}h$
which works out to be a slightly wrong version of Velocity verlet i think.
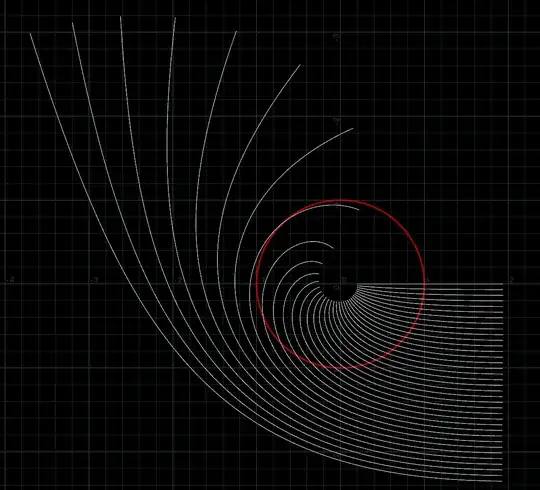
Just experimentally, i know at least for this formulation $r_d = \frac{GM}{c}$ is correct as can be seen here;
You can see 36 rays being shot parallel to the Horizon. The Horizon is marked with the red ring for $G=M=c=1$. This is also kinda in line with a Vox video where they said the deflection of light predicted by Newtonian mechanics is half of GR´s.
So whilst this appears to be true on a "experimental" level, i kinda struggle to see where the $\frac{GM}{c}$ comes from. Or if this is a case of me being right, for the wrong reason. My question(s) boil down to if this is a sensible approach and if my results are "true", within the bounds of what constitutes true for a Darkstar. And like maybe where $r_d = \frac{GM}{c}$ comes from.
On the side, if we actually compare the Darkstar to Schwarzschild (Kerr metric with $a = 0, M = 1, G = 1$) they are remarkably similar, if $M = 2$ for the Darkstar.
Alright then, thanks for reading and hopefully my math did not violate to many human rights.
EDIT;
I am working on a Visualization of what i am doing in the program, exactly. In the meantime a lot of the discussion in the comments seems to be focused around the escape velocity. Which as far as i can see is not relevant here because by normalizing everything the velocity is constant.