Dynamics of a mass-spring system with non-ideal spring

Question

Show that a mass attached to a non ideal spring that has a restoring force given by $-kx-ax^3$, where $x$ is the displacement from the equilibrium position, executes a periodic motion. What's the period of this motion? Is it harmonic (simple harmonic motion)?

So, to show that the movement is periodic I guess I would need to solve the differential equation $mx''+kx+ax^3=0$ by Newton's second law. Is that right? I think there might be a better approach since this shouldn't be a difficult problem and should be solvable even for students that don't have a background on differential equations, but I can't get it right.

Answer 1

Starting with the differential equation

$$m\,\ddot x+\,F(x)=0\tag 1$$

where $~\,F(x)=k\,x+a\,x^3~$

you can see the numerical solution with the initial conditions $~x(0)=x_0~,\dot x(0)=0~$ at this figure :

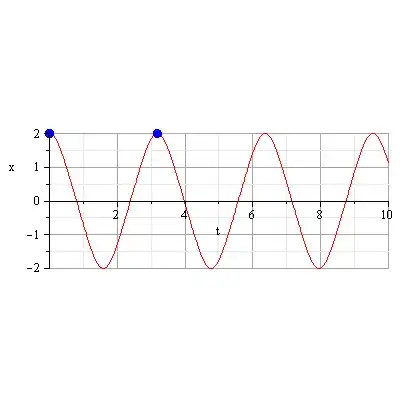
$~x(t)~$ is periodic motion but the period is depending on the amplitude of $~x(t)~$ which is $~x_0~$ , thus it is not simple harmonic motion

What's the period of this motion?

we want to obtain the time $~T~$ between the two blue points .

The period T

multiply equation (1) with $~\frac{dx}{dt}~$ and integrate you obtain the energy $~E=T+U~$

$$ E=\frac m2 \left(\frac{dx}{dt}\right)^2+U(x)\tag 2$$

where $~U(x)=\frac 12 k\,x^2+\frac 14 a\,x^4~$

at $~t=0~$ ,$~\frac{dx}{dt}=0~,x=x_0~$ thus $$E_0= \frac 12 k\,x_0^2+\frac 14 a\,x_0^4$$

solve the equation $~E=E_0~$ for $~dt~$ you obtain

$$dt=\pm 2\,{\frac {m{\it dx}}{\sqrt {-2\,m \left( 2\,{x}^{2}k+a{x}^{4}-2\,{x_ {{0}}}^{2}k-a{x_{{0}}}^{4} \right) }}} $$

from here the period $~T~$ is

$$T=\pm 4\,\int 2\,{\frac {m{\it dx}}{\sqrt {-2\,m \left( 2\,{x}^{2}k+a{x}^{4}-2\,{x_ {{0}}}^{2}k-a{x_{{0}}}^{4} \right) }}} $$

the result is "elliptic integral "

$$T=\pm 4\,\sqrt {m}{\it EllipticF} \left( {\frac {x}{x_{{0}}}},{\frac {ix_{{0 }}\sqrt {a}}{\sqrt {2\,k+a{x_{{0}}}^{2}}}} \right) \sqrt {2}{\frac {1} {\sqrt {2\,k+a{x_{{0}}}^{2}}}}\bigg|_{x=x0}^{x=0} $$

with the data of the above figure $~|T|=3.179~$

---

$$\dot x\,m\,\ddot x+\dot x \,F(x)=0\\ \frac m2 \frac{d}{dt} \left(\dot{x}^2\right)=-\frac {dx}{dt}\,F(x)\\ \frac m2 {d} \left(\dot{x}^2\right)=-{dx}\,F(x)\\ \frac m2 \int {d} \left(\dot{x}^2\right)=-\int {dx}\,F(x)$$

Answer 2

Since no external forces are jerking off, the work is conservative and the energy remains the same for all instant of time. Hence, there must be a potential function $U$ which verify that $\vec{F} = - \vec{\nabla} U$.

With this sense, let $U(x) = \frac{1}{4} a x^4 + \frac{1}{2} k x^2$. Is not so difficult to verify that $U(x)$ represents a stable potential distribution since its concavity is positive. Therefore, $x$ does not diverge. Two options left: or $x$ is an oscillator or it reaches a steady value. Now, the total energy is:

$$E_0 = K(x) + U(x) = \frac{1}{2} m \left(\frac{dx}{dt} \right)^2 + \frac{1}{4} a x^4 + \frac{1}{2} k x^2$$

If $x$ reaches a steady value, this means that all the derivatives go to zero as t goes to infinity. The only possibility for this is that $x_\infty = 0$, otherwise $\sum \vec{F} \neq \vec{0}$. Replacing in the energy equation, we note that only the trivial solution with $E_0 = 0$ fulfills the condition. But we are interested in $E_0 > 0$, and then the system does not reach a steady value. But since $x(t)$ remains bounded, then $x(t)$ is periodic. The points of maximum elongation are where $x' = 0$:

$$E_0 = \frac{1}{4} a x^4 + \frac{1}{2} k x^2$$

$$\pm x_{MAX} = \pm \sqrt{\frac{\sqrt{4 E_0 a + k^2} - k}{a}} $$

The next step consists in finding $dt$ as a function of $x$, from the energy equation. Integrating from $-x_{MAX}$ to $x_{MAX}$ we get one half of the period:

$$dt = \sqrt{\frac{m}{2}} \frac{1}{\sqrt{E_0 - \frac{1}{4} a x^4 - \frac{1}{2} k x^2}} dx$$

$$ \int_0^{T/2} dt = \sqrt{\frac{m}{2}} \int_{-x_{MAX}}^{x_{MAX}} \frac{dx}{\sqrt{E_0 - \frac{1}{4} a x^4 - \frac{1}{2} k x^2}} $$

(good luck solving that)

Finally, the oscillator is not harmonic since the ODE is not linear.

Answer 3

Any time you have some acceleration defined as a function of position only you can always find the speed-distance relationship using the following direct integration

Given acceleration ${\rm acc}(x)$ omly

Subject to IC

$$ v(0) = v_0 $$

and

$$ x(0) = x_0 $$

First, integrate $ \underline{ v {\rm d}v = {\rm acc}(x) {\rm d}x }$ over distance

$$ \tfrac{1}{2} v^2 - \tfrac{1}{2} v_0^2 = \int \limits_{x_0}^x {\rm acc}(x) \,{\rm d}x $$

Then solve for $v$

$$ v = \sqrt{v_0^2 + 2 \int \limits_{x_0}^x {\rm acc}(x)\,{\rm d}x } $$

and possibly find the time-distance relationship with

$$t = \int \limits_{t_0}^t \frac{1}{v} {\rm d}x = \int \limits_{t_0}^t \frac{1}{\sqrt{v_0^2 + 2 \int \limits_{x_0}^x {\rm acc}(x)\,{\rm d}x }} {\rm d}x $$

For your case

$$ \tfrac{1}{2} v^2 - \tfrac{1}{2} v_0^2 = \int \limits_{x_0}^x \left( - \tfrac{k}{m} x - \tfrac{a}{m} x^3 \right) \,{\rm d}x = - \frac{ \tfrac{a}{2} (x^4-x_0^4) + k (x^2-x_0^2)}{2 m} $$