Topological proof of spin-statistics theorem confusion

Question

I am currently studying the spin-statistics theorem. I have found a section on John Baez's website which presents a "proof" of the spin-statistics theorem. He states the theorem as:

This is a little grab-bag of proofs of the spin-statistics theorem. Quantum mechanics says that if you turn a particle around 360°, its wavefunction changes by a phase of either +1 (that is, not at all) or -1. It also says that if you interchange two particles of the same type, their joint wavefunction changes by a phase of +1 or -1. The spin-statistics theorem says that these are not independent choices: you get the same phase in both cases! The phase you get by rotating a particle is related to its spin, while the phase you get by switching two goes by the funny name of "statistics". The spin-statistics theorem says how these are related.

Then, he states the proof as:

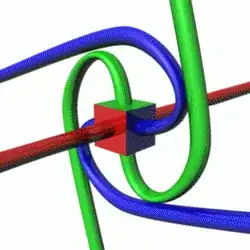
The "proof" is topological, in that if you rotate a thing (particle) with strings all over it, the strings are all twisted after 360 degrees of rotation, but after 720 degrees the strings can be untangled without moving the object. Similarly, if two things (particles) connected by lots of strings are interchanged, the strings are left twisted up exactly as if one particle had been rotated by 360 degrees. So the conclusion is that interchanging two particles is topologically indistinguishable from a rotation of one particle by 360 degrees — a particle which changes sign after a rotation will be antisymmetric with respect to pairwise interchange.

However, I think I am vastly misunderstanding this argument. First, I do not understand why, if particles were connected by strings, interchanging them would result in the strings being twisted. Secondly, I don't understand why after 720 degrees the strings can be untangled without moving the object. Third, which might be the general underlying confusion, I don't see what axis these rotations are about in general.

Is there a way to understand this argument more explicitly?

Answer 1

You can demonstrate this to yourself by placing a coffee cup in the palm of your outstretched right hand. Now bring your arm in towards your body and swivel your palm around under your elbow and then out in front of you again, thereby rotating the coffee cup through 360 degrees. But note that your arm is now twisted around its axis. How to get rid of the twist? Bring your palm back towards your head and pass it over the top of your head, and swing your arm around to bring your palm with the coffee cup out in front of you again- thereby rotating it through another 360 degrees, and eliminating the twist.

Because of the twist that your arm gets during the first 360 degree rotation, it takes another 360 degree turn to untwist it and thereby bring the coffee cup back to its original position: 720 degrees to get back to your starting point.

And it's because your arm is connected to the cup.

Answer 2

The Wikpedia page on orientation entanglement has a bunch of pictures displaying this situation. You're supposed to imagine objects attached to far walls and each other by elastic strings, and consider how these strings coil and uncoil as you rotate or exchange the objects:

When these strings are attached to another object, then when you exchange the two objects the string has to twist in the same way as during a full rotation - try to imagine the blue string in the picture above attached to another cube and then moving the two cubes to exchange their positions without rotating the cubes: the blue string then has to twist during this motion.

That these strings always become untangled after 720° rotations is the "topological" part: The rotation group $\mathrm{SO}(3)$ is not simply connected, but its double cover is. When we look at the orientation of objects over time, we're looking at paths in the rotation group because an orientation is specified by an ordered orthonormal basis (e.g. the three vectors normal to the cube faces).

The path traced out by a 360° rotation arrives back at the same orientation, i.e. is a loop in $\mathrm{SO}(3)$ but it is not null-homotopic. Meanwhile, the path traced out by a 720° rotation is, meaning there is a continuous deformation from this loop to the do-nothing loop. Moving along this homotopy gives a way to restore the original untangled state of the strings without rotating the cube again (see also WillO's explanation of this for the case of the plate trick here), so the strings are not really tangled after 720° rotations.