What would happen if you threw an object (a tennis ball for example) at a white hole?

Question

I know white holes are hypothetical but IF they were real, what would happen if you threw an object at the white hole ? will the object get repelled as soon as it gets close to the white hole or will something else happen ?

Answer 1

The tennis ball would fall into the black hole.

Black holes and white holes are different parts of the same object: the eternal black hole. To keep the maths simple, we consider the case of a spherically-symmetric solution that never changes, so it exists forever into both the future and past. (Obviously that can't work in our universe, because of the big bang, but this is just a mathematical model.)

The original Schwarzchild solution considered the question of where the tennis ball would end up. It turns out that spacetime twists towards the hole so that time points inwards, into the black hole. When the entire future lightcone is tilted inwards, there is no escape. The black hole's event horizon cannot be seen from the outside, because every part of it is in the future of every observer outside the horizon.

However, there is a big problem with this solution, which arises when we instead ask where did the tennis ball come from?

We can trace the trajectory of a tennis ball in freefall forwards in time, and it always ends up in the black hole. But what if we trace its trajectory backwards in time, and ask how a freefall tennis ball could have got there? We can easily do so part of the way - it's like if we throw a tennis ball up into the air here on Earth: it travels outwards, comes to a halt, and then falls back to Earth. So out in space the tennis ball trajectory when traced back must be coming out of the black hole. But how is this possible? Black hole event horizons are one way, surely?

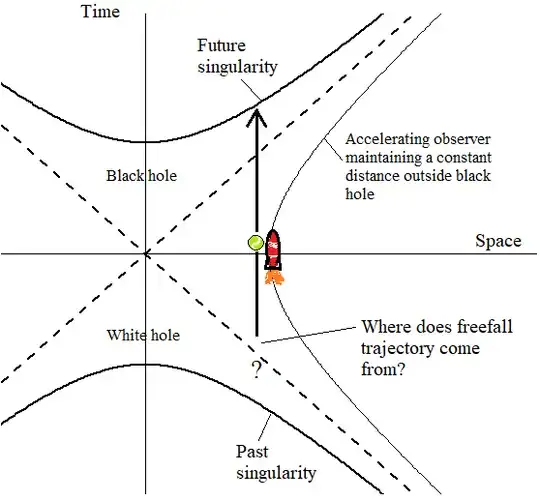
It turns out that there is a solution to this apparent paradox, which is that we can take our existing future-only black hole solution, make a copy, time-reverse it, and glue the two together back to back. The black hole event horizon is in the future. There is a different event horizon now in the past. It's time-reversed, so all the lightcones tilt out of the region. And it has another singularity at its centre which is the start of time, just as the singularity in the future event horizon is an end to time.

In the figure, spacetime is divided into four quadrants by the dashed diagonal lines, which are the event horizons. Time moves up the page. Radial distance from the centre of the black hole is shown horizontally. We have warped the scales so that lightcones point upwards everywhere on the diagram and the speed of light is represented everywhere by $45^\circ$ lines. The original Schwarzchild solution only included the top and right quadrants, which leaves open the question of where freefall trajectories come from. If you tilt your head to the right $45^\circ$, you can see the usual spacetime picture as seen by a distant observer, with the singularity on the left at $r=0$, the event horizon drawn vertically, and the outside universe to the right of it. The bottom quadrant and left quadrant are the time-reversed black hole we have glued on, with the bottom quadrant being the white hole.

Since hypothetical particles can only come out of the region, we call it a white hole. But since we generated this solution by assuming that nothing changes, we have to posit that nothing ever does. The past singularity must be of a nature such that it can't progress into the future. It has a huge mass - it is the true source of the eternal black hole's gravity, as felt by the outside universe. (We can only sense the past, not the future, and the singularity is in everybody's future.) But it is totally dark. It is, in fact, precisely what we are looking at when we look directly at an eternal black hole. Any photons we see, like tennis balls, have to come from the direction of the hole.

Real astrophysical black holes don't have, or need, a white hole in their past. Tracing trajectories back in time lead back to the collapsing star. The gravity we feel comes from the star as it collapses, the light we see is the star's light infinitely red-shifted. The shape of spacetime changes with time, making the maths much harder. The white hole is what the collapsing star turns into if we push the collapse back in time to infinity, to get a black hole that has always existed.

A white hole is just the past part of a hypothetical black hole that has existed forever. It is the other end of all the freefall trajectories, that finish up in the black hole. Since a white hole is a black hole, the tennis ball ends up exactly where you expect: in the future singularity of the black hole.