I have been following recent work by Susskind [1,2] where he talks about fact that the volume inside an eternal black hole increases with time. I am unsure how to obtain this result. I'll show my attempt and ask questions in the end.
My approach
The metric in Kruskal-Szekeres coordinates is
\begin{equation} ds^2 = \frac{32G^3 M^3}{r}e^{-r/r_s}\big(-dT^2+dX^2\big)+r^2 d\Omega^2 \end{equation}
where the Schwarzschild coordinate radius $r$ can be expressed as
\begin{equation} r=r_s \big[1+W_0 (\frac{X^2-T^2}{e})\big] \end{equation}
where $W_0$ is the Lambert function. I want to calculate the volume of slices at fixed $T$, the metric determinant for these 3-volumes would be
\begin{equation} \det\big[g_\text{induced}\big]=\frac{32G^3 M^3}{r}e^{-r/r_s}r^3 \sin^2 (\theta) \end{equation}
So the volume I want is
\begin{equation} V=4\pi 32G^3 M^3\int_{-T}^{T}e^{-r/2r_s}r^{3/2}dX \end{equation}
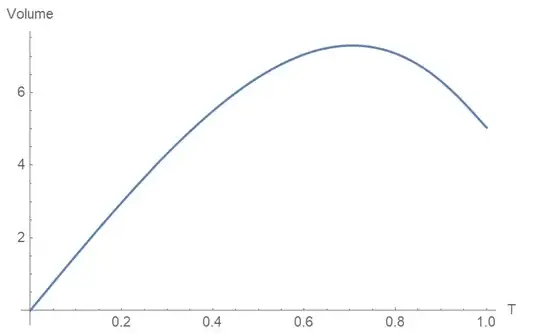
where $r$ is implicitely a function of $X$ and $T$. Of course, at $T=1$ these surfaces will hit the singularity, so I guess this notion of 3-volume would only work for $T$ less than 1. The volume I get by integrating this in Wolfram is
My questions are:
Why does this decrease even before hitting the singularity?
Are there coordinates that foliate the inside in hyperboles, such that they cover it from horizon to singularity fully? I think that the fact that these foliations get cut after $T=1$ is a problem.