There is no formula for the half-life of a CO$_2$ molecule in the air that depends only on temperature and pressure and the equilibrium concentrations in the air and water.
At the very least, you also need to know the mixing time for CO$_2$ in the air volume above the water, since a CO$_2$ molecule has to reach the water surface before it has any chance of passing through it. For a perfectly static system with no air or water movement - which is hard to achieve experimentally - the average time for a CO$_2$ molecule to reach the water surface would roughly be the diffusion time $t=h^2/D$, where $h$ is the average height of the air above the water and $D=16\times10^{-6}\,\mathrm{m^2/s}$ is the diffusion constant for $\mathrm{CO_2}$ in air. For the Earth's atmosphere with a scale height of about $8.5$ km, $t\sim 10^5$ years.
Because atmospheric mixing does not depend on diffusion, but instead is driven by winds, convection, storms, and other air movements, the actual atmospheric mixing time is only about a year.
In case you are trying to model CO$_2$ transfer between the Earth's atmosphere and ocean, note that simple models are hopeless. The transfer rate also depends on wave motion, surfactants, salinity, turbulence, bubble production, ocean layering, …. See, for example, this MIT Open Course lecture on "Marine Chemistry: Dissolved Gases and Air-sea exchange".
The actual CO$_2$ atmospheric residence time is roughly 5-10 years.
Edit added after motivation and assumption of question clarified by OP.
Sea-air CO$_2$ exchange flux $F$ is typically modelled as
$$F=k \Delta C$$
where $\Delta C$ is the air-sea CO$_2$ concentration difference. and $k$ is the "piston velocity" (i.e. the gas transfer velocity). This turns out to roughly depend on the wind velocity squared. Models for the gas-exchange process usually assume there is a thin boundary layer at the surface of the ocean where the gas exchange takes place, with mixed bulk atmosphere and ocean above and below. For example in a stagnant boundary layer model, the layer might be about 20 microns thick and $k\sim 5$ m/d, so it would take about a thousand days for a $5$ km deep ocean to exchange its CO$_2$. Better models include film replacement and eddy impingement.
Oceanic CO$_2$ partial pressures range from pCO$_2$~100 μatm to ~1000 μatm, so the ocean is locally a CO$_2$ source or sink depending on whether ocean pCO$_2$ is greater or less than the atmospheric pCO$_2$ of ~400 μatm, and the rate depends on how strong the wind is blowing and other factors.
To accurately understand sea-air CO$_2$ exchange requires complex modelling based on lots of ocean and atmospheric measurements, and as shown in IPCC 2021 Figure 5.9(a) , the ocean is typically a CO$_2$ source in the tropics and a sink in higher latitudes.
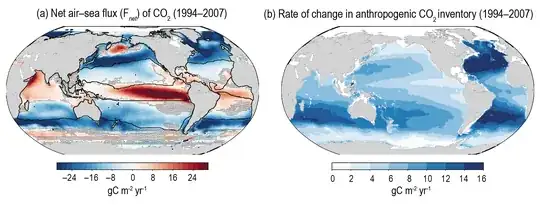
Figure 5.9(b) on the right shows the rate at which anthropogenic CO$_2$ is being stored in the oceans.
