How does a violin produce notes, microscopically?

Question

I believe this question would have been asked before, but not like this. The popular answer to this question is that the slide-release action of a bow sets up vibrations in the strings, of which ultimately only the resonant frequencies would survive.

Plucking a guitar string sets up a transverse oscillation on the strings at its resonant frequencies. But when you play a violin, you slide a bow over the strings. We know that the strings first attach to the bow, then release once the static friction is overcome, and this process repeats again and again. But how does this process ensure periodicity? We don't hear a discontinuous noise from a violin; rather we hear smooth continuous notes.

How do the strings know when to catch the bow, and when to release them ?

Answer 1

Of course, the bow string does not know when to attach and release a violin string, it is the choice of materials which dictates this.

When viewed under a microscope it is possible to see the tiny barbs on the surface of each hair which in themselves do not make the string vibrate. The addition of rosin, which is sticky, to the bow hair increases friction between the bow hair and the strings on the instrument causing the strings to vibrate as the bow hair is drawn across the surface of the strings.

Now to (partially) answering the question,

How do the strings know when to catch the bow, and when to release them?

As you might expect the answer is complex, but I will try and give you an idea of what happens.
Helmholtz, after observing the motion of strings with a vibration microscope discovered that the motion of the string could be described by a sharp corner, traveling back and forth on the string along a parabola-shaped path.
The fundamental period of vibration $T$ is determined by the time it takes for the corner to make a single round trip.

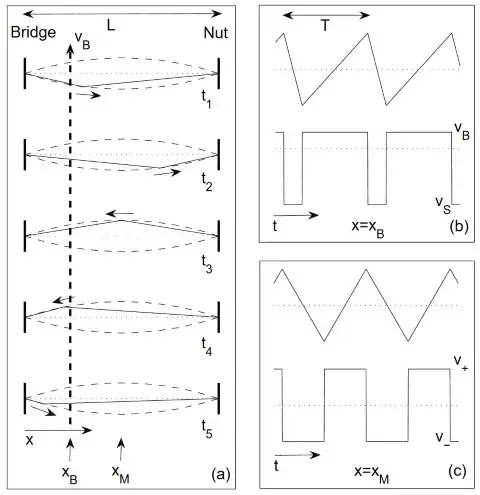
Imagine a triangular wave travelling along the string and then being reflected at the ends.
At the bowing position the bow velocity is $v_{\rm B}$ and the string has two velocities, $v_+$, when no slipping occurs (the bow sticks to the string) and so $v_+=v_{\rm B}$, and $v_-$ when there is slipping between the bow and the string.

It is the movement of the travelling corner along the string which synchronizes the slipping and sticking phases and is the reason,

We don't hear a discontinuous noise from a violin; rather we hear smooth continuous notes.

Referring to the diagrams and graphs above, the left hand diagram has a sequence of sharp corner wave profiles ("photographs" of the string at various instances of time) with the bow at position $x_{\rm B}$ travelling with velocity $v_{\rm B}$ and the middle of the string at position $x_{\rm M}$.
The graphs on the right hand side at graphs of string displacement and string velocity as a function of time at the bowing position (b) where the string velocity is either equal to the bow velocity, $v_+=v_{\rm B}$ or the string is slipping relative to the bow, $v_-=v_{\rm S}$.
At the middle, $x=x_{\rm M}$ the $v+$ and $v_-$ just represent the string velocities which on this simplistic model means that the position of bowing has no effect.

This analysis assumes no losses and ignores the stiffness of the sting and the role of the bow force all of which which require more sophisticated models resulting in rounded corners and resharpened corners.

As a late addition to my answer I have "borrowed" @Quantumwhisp's excellent gif,

and the link to the article Science and the Stradivarius in Physics World.
I hope they do not mind.

Answer 2

We don't hear a discontinuous noise from a violin; rather we hear smooth continuous notes.

You're taking that for granted. You can produce a discontinuous noise from a violin quite easily, and all beginners do, but violinists strive not to. It is not a given that just dragging a bow across a violin string will produce a continuous tone. To properly sound a note the appropriate combination of pressure and bow speed is required. If you change one then you must adjust the other (for example, to play at different volumes). The pressure and bow speed combination required are also different for every note, and for the location on the string that is being bowed.

For example, if your bow pressure is too high and your bow speed is too slow the stick and slip does not happen properly and you get a screeching, scraping sound as the slip and stick process is constantly interrupted. I am not entirely clear about the exact the role of the speed but this is most evident when playing a low note on a low string, especially on a cello because the amplitudes are larger and the oscillations are slower and easier pick out by the sense of touch. When pressure is too high and bow speed is too slow, you can see, hear and feel the string slip but then stick somewhere midway between the endpoints of the "correct" oscillation.

It almost seems like when bow pressure is too high and bow speed is too slow, the string is insufficiently tensioned. That is, it seems like the faster bowing is able to tension the string more during the stick phase before it slips, thus providing more energy to the string such that it can reliably escape the static friction at the opposite oscillation end point. This theory seems consistent with how bowing closer to the bridge where the effective tension is higher since the strings have less freedom to be deformed (you get a greater increase in tension for the same lateral displacement). That is, when bowing closer to the bridge, increased bow pressure and reduced bow speed is required relative to bowing farther from the bridge.

So really, the violinist is adjusting and optimizing bow parameters in real-time such the string's stick and slip falls in line with an oscillation that produces a continuous note. It doesn't just happen on it's own.

Answer 3

But how does this process ensure periodicity?

On its own, it doesn't. The bow acting on the string produces vibrations that are effectively broadband noise — you can check this by muting the string with your fingers while dragging the bow across it. The sound you hear won't have any clear tone to it, and on a spectrogram it would contain a wide range of frequencies.

The string's tension and its boundary conditions (being pinned by the bridge near one end, and either pinned by the nut on the other end, or pinned against the fingerboard by a finger) give it a resonant frequency, and the resonance acts like a filter. The excitation frequencies from the bow that "agree" with this resonance are reinforced and amplified, while the other frequencies are attenuated and dissipated. This filtering is very effective (in terms familiar to electronics engineers, a violin string has a Q-factor of around 1000 at its fundamental frequency), which means that most of the energy provided by the bow becomes sound at one of the resonant frequencies. The exact relationship between the different resonant frequencies gives the instrument its tone.

None of this is really very different from a plucked or picked string (whether guitar or violin); plucking a string is approximated as an impulse (energy provided at an instant) which also contains a wide array of frequencies (theoretically, every frequency), and it's the filtering provided by the string's resonance that turns that impulse into a clear note. The incomplete filtering at the very moment of the pluck is part of what gives a plucked string its sound. But the biggest difference, of course, is that bowing provides a continuous input of energy, allowing sustained notes of constant volume or even ones that increase in volume as they go, while plucking provides all of the energy up front, and then the note decays in volume as the string loses energy.

Answer 4

What is a mystery to you is actually very simple. The bow inputs a signal containing lots of frequencies to the string, because the friction between bow and string is very noisy. Noise is a random signal containing lots of frequencies (see: Fourier transformation), it is very wide banded. Then, because of the filtering by the string, you will hear, through the air, just the string's resonance frequency.

You don't need to enter a continuous random noise signal with a bow for this to work. You could also enter a step signal, by plucking the string, just like on a guitar, or by slamming it, like in a piano, or a percussion instrument. The step signal can also be decomposed to an infinite number of sinus signals with different frequencies. Just lookup: Laplace transformation.