The pressure at a point inside a static fluid is same in all directions because the the collisions of particles take place isotropically.
However, at the same time pressure increases with depth. So downward pressure must not be equal to upward pressure at that point.
This two statements are contradictory and I am really confused.
What is the problem in my understanding of the topic?
Suppose that we consider an element of fluid, density $\rho$, of sides $\delta x,\,\delta y$ and $\delta z$ as shown in the diagram below.
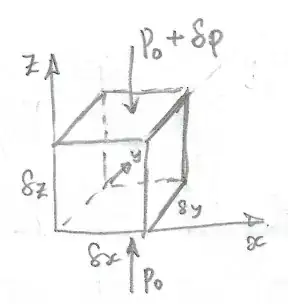
The arrows adjacent to pressure labels, $P_0$ and $P_0+\delta P$, indicate the directions of the forces on the element which have magnitudes, $P_0\,\delta x\,\delta y$ and $(P_0+\delta P)\,\delta x\,\delta y$ due to the pressure at $z$ and $z+\delta z$ respectively.
If the element is assumed to be in equilibrium the net force on it must be zero,
ie $P_0\,\delta x\,\delta y - (P_0+\delta P)\,\delta x\,\delta y-\delta x \,\delta y\,\delta z \,\rho\,g=0 \Rightarrow \dfrac {\delta P}{\delta z} = - \rho \,g$
and if $\delta z \to 0$ then $\dfrac {dP}{dz} = - \rho \,g$ which is called the hydrostatic equation.
I imagine that you were considering a point, which has no dimensions, in the fluid, where you could say that the pressure was $P_0$ and there was also a rate of change of pressure with respect to height, $z$.
The issue you are having is a problem of scale. You are completely correct that if you were to take a small “box” of the fluid from the bulk, the pressure exerted on the upper and lower portions of the fluid would not be equal, but only nearly equal. But in the limit that this fluid “box” becomes infinitesimally small, so too does the difference in the pressure between the upper and lower portions. In your case, you refer to a “point,” which has no dimensionality and therefore you are utterly incapable of discerning any pressure differential. Of course you are right that the pressure is isotropic when looking side to side, as the gravity experienced should be the same. Interestingly, if you zoom in to a molecular scale you will run into the interesting question of whether it even makes sense to talk about pressure anymore, as the interactions now appear much more local and you can only talk about an average pressure. Just a bit of food for thought.
I also think that the point made in an earlier comment is important to reiterate. Pressure is a scalar, nor a vector. This means that pressure depends on the magnitude of the force exerted on some unit area, not what direction you are measuring that force from. More technically, you would have to specify axes and define the stress tensor if you wished to do a more rigorous analysis of some directionally dependent phenomena. But in your case it is perfect consistent to define the pressure at any given point in space and be done with it.
