If two opposite charges are moving at a velocity of $0.9c$ relative to a laboratory, but are at rest relative to each other (say the charges are moving in parallel), will there be any relativistic corrections to electrostatic attractive force (given by Coloumb's law) exprienced by the charges? In a frame in which the particles are at rest, Coloumb's law would be valid, but in the laboratory frame, the charges, being opposite, would act as antiparallel currents which repel each other. This would lead, I believe, to a reduction in electrostatic attraction on the order of $\gamma^{2}$, where $\gamma = \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$ (cf. https://www.phys.unsw.edu.au/einsteinlight/jw/module2_FEB.htm this works out the equivalent problem but for like, i.e. same sign, charges), but only as viewed from the laboratory frame. Is there any relativistic correction to the frame in which the charges are stationary? I would expect not, but I was just wondering if there is something that I am missing given the relativistic speed of the two particles?
2 Answers
$ \newcommand{\bl}[1]{\boldsymbol{#1}} \newcommand{\e}{\bl=} \newcommand{\p}{\bl+} \newcommand{\m}{\bl-} \newcommand{\mb}[1]{\mathbf {#1}} \newcommand{\mr}[1]{\mathrm {#1}} \newcommand{\gr}{\bl>} \newcommand{\les}{\bl<} \newcommand{\plr}[1]{\left(#1\right)} \newcommand{\Vlr}[1]{\left\Vert#1\right\Vert} \newcommand{\vp}{\vphantom{\dfrac{a}{b}}} \newcommand{\hp}[1]{\hphantom{#1}} \newcommand{\x}{\bl\times} \newcommand{\tl}[1]{\tag{#1}\label{#1}} $
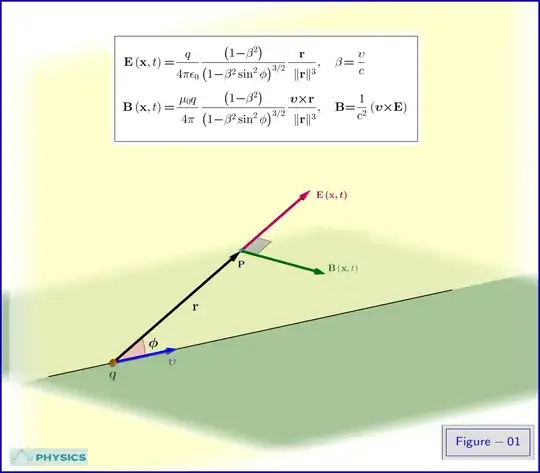
The relativistic equations for the electromagnetic field of a uniformly moving electric charge $\:q\:$ (see Figure-01) are :
\begin{align} \mb E\plr{\mb x,t} & \e \dfrac{q}{4\pi\epsilon_0\vp}\dfrac{\plr{1\!\m\!\beta^2}}{\plr{1\!\m\!\beta^2\sin^2\!\phi}^{3/2}\vp}\dfrac{\mb r}{\:\:\Vlr{\mb r}^3},\quad \beta\e\dfrac{\upsilon}{c} \tl{01a}\\ \mb B\plr{\mb x,t} & \e \dfrac{\mu_0 q}{\hp{\epsilon} 4\pi\hp{_0}\vp}\dfrac{\plr{1\!\m\!\beta^2}}{\plr{1\!\m\!\beta^2\sin^2\!\phi}^{3/2}\vp}\dfrac{\bl\upsilon\x\mb r}{\:\:\Vlr{\mb r}^3},\quad \mb B\e\dfrac{1}{c^2}\plr{\bl\upsilon\x\mb E}\vphantom{\dfrac{a}{\dfrac{}{}b}} \tl{01b} \end{align}
The "Correction Coefficient" of the electric field (modified Coulomb field) is \begin{equation} \mr{CC} \e \dfrac{\plr{1\!\m\!\beta^2}}{\plr{1\!\m\!\beta^2\sin^2\!\phi}^{3/2}\vp} \tl{02} \end{equation}
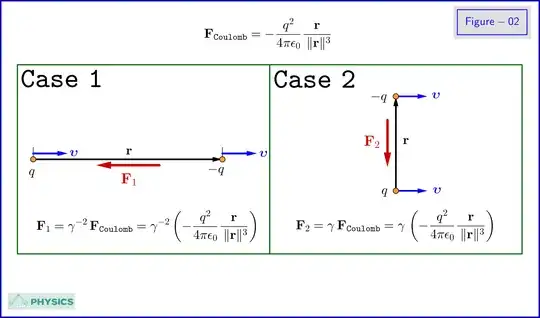
So, \begin{equation} \mr{CC} \e \left. \begin{cases} \gamma^{\m 2}\!\!\!\!\!\!& \les 1 \quad \texttt{in Case 1 : } \mb r\,\bl \| \,\bl\upsilon \bl\implies \phi\e 0\\ \:\:\:\gamma & \gr 1 \quad \texttt{in Case 2 : } \mb r\bl \bot \bl\upsilon \bl\implies \phi\e \pi/2\\ \end{cases} \right\} \tl{03} \end{equation} as shown in Figure-02.
- 16,825
- 2
- 45
- 73
The total force is reduced by a factor $\gamma$ in the frame where the charges are moving.
This assumes that the charges have a common rest frame. In this frame the power transferred from one charge to the other vanishes, hence the four force is $$f^\mu = \left(0,\bf f\right)$$ with $f= {{\bf r} \over {4\pi \epsilon_0 r^2}} $ transforms into $$f’^\mu = \left(-\gamma {\bf v} \cdot {\bf f},\gamma {\bf f}\right).$$ Note that a power $f’^0$ appears unless the velocity is at right angles to the separation.
- 27,443