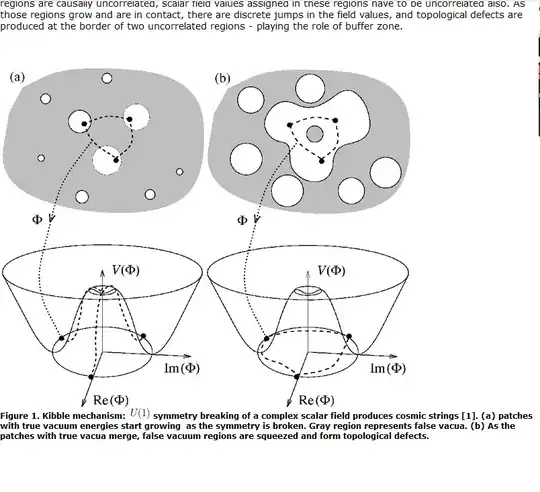
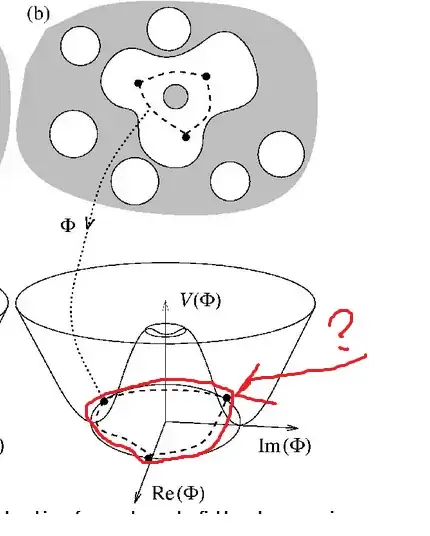
I have a lot of troubles to understand heuristically the principle behind Kibble's model for genesis of cosmic strings via Kibble mechanism. More precisely I not understand how to interpret following two pictures I found here:
Prelude: We start with usual Higgs field $\Phi$ with brocken $U(1)$-symmetry with model Lagrangian of the shape
$$ \mathcal{L}= \frac{1}{2}(D_{\mu}\Phi)^{\dagger}(D^{\mu}\Phi) - \frac{1}{4}F_{\mu \nu}F^{\mu \nu}-V(\Phi)$$
where $F_{\mu \nu}$ is the field strength tensor associated with the
vector gauge boson $A_{\mu}$, the $D_{\mu}= \partial_{\mu} +igA_{\mu}$ the covariant dirivative with respect the gauge and $V(\Phi)= a \cdot (\vert \Phi \vert^2- \eta_{\nu}^2)^2 $
where $\eta_{\nu} \neq 0$ the degenerated vacuum
expectation value of the Higgs field $\Phi$. Therefore the vacuum manifold $S^1 \cong U(1)$ can be parametrized ba $\eta_{\nu}e^{i \theta}$, $\theta \in [0,2\pi)$
Key Questions:
In the upper two pictures (a) and (b) with grey background & white circles: Which kind of "space" is preciesely depicted there? The configuration space of states or the spatial space (="domain" of wave functions)
in the right picture at the bottom: which meaning has the red marked dotted trajectory? It looks strange because it seemingly not lies on the graph of $V(\Phi)$
which state function $\Phi$ is depicted there? An arbitrary one or such one coming from the "old" vacuum and after cooling down becoming frustrated
What is here meant concretely by "false vacuum"?
Finally: what is in this context precisely meant by topological defects (like eg cosmic strings): literally some defects is the space as depicted in a) and (b) (...and in which space do they "live"? The space of configurations of states or the "spatial" space) or certain solutions of the equation of motion ("solitons"). If the later is the case: why they are called "topological" defects?
Upshot: To forestall the legitimate objection that there are too many questions posed, it should be said that morally the concern of this question can be concisely summarized as "What are the depicted dashed trajectories in the picture, in which space do they live ( ...spacetime, configuration space?) and which role do they play in Kibble mechanism?"