0

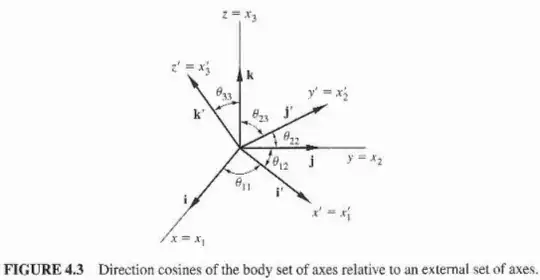
In section 7.2, about the Lorentz transformations, the H. Goldstein book states that given two inertial frames with a relative velocity $\textbf{v}$, the Lorentz transformation associated is given by the matrix $\textbf{L}$, where this matrix is said to be a proper transformation (see the subsection "Proper transformations" of the "Mathematical formulation" in the Wikipedia page for the explicit expression of $\textbf{L}$).

In the next page, however, it also states that the most general Lorentz transformation is given by the product $\textbf{RL}$ where $\textbf{R}$ is a rotation matrix.

What does this matrix represent? I guess it's a change of basis, but I am not quite sure.

sconsolato
  • 11
  • 2

1 Answers1

1

$\mathbf{R}$ is an orthonormal rotation matrix transforming from $xyz$ coordinates to $x'y'z'$ coordinates (as in Goldstein's chapter 4).

enter image description here
(image from Goldstein "Classical Mechanics")

The only thing needed be added here because of relativity is an additional row/column for the time coordinate $ct$. So the matrix becomes: $$\mathbf{R}=\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & R_{xx} & R_{xy} & R_{xz} \\ 0 & R_{yx} & R_{yy} & R_{yz} \\ 0 & R_{zx} & R_{zy} & R_{zz} \end{pmatrix}$$ In 4-dimensional spacetime this transformation represents a spatial rotation without affecting time.

Thomas Fritsch
  • 42,352