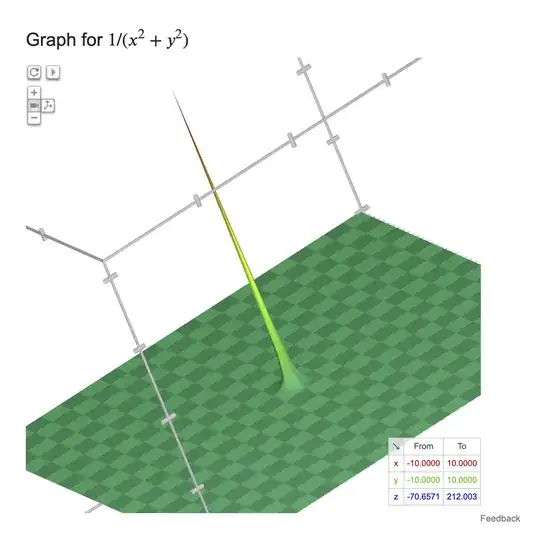
A great many curves (described by exponentials, logarithms, powers, trigonometric functions, etc.) might be fit to the contour of any particular natural phenomenon. Alternatively, there are published "atlases" of surfaces of revolution:
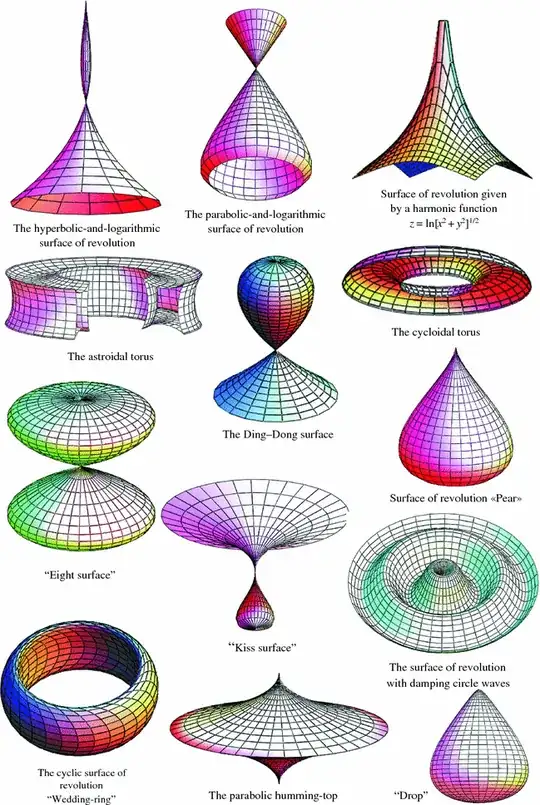
Undirected curve-fitting and shape-matching can provide a useful closed-form analytical expression but may not provide insight into the underlying processes.
As an alternative, we might propose a hypothesis based on biophysical principles and see where it takes us.
Although I've never studied algae growth specifically, based on a research background in mechanical engineering, materials science and biophysics, it occurs to me that the features resemble at least two other distinct features, and a commenter has helpfully described a third scenario:
(1) The constant-stress hanging rod loaded by self-weight only.
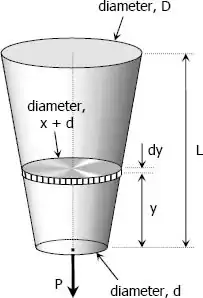
(All images from quick online searches of the relevant keywords.)
A classic statics problem is to design a rod or wire, hanging from its own weight, such that its internal stress is everywhere constant. Here, the cross-section area must increase when moving up because the applied weight progressively increases. This problem has enormous importance in the prospective design of a space elevator, where we find that existing materials would require an impossibly large cross section for the required height.
To summarize the problem, for a height-dependent radius $r(z)$, the weight below any vertical position $z$ is $W(z)=\int_0^z \rho\pi r(z^\prime)^2\,dz^\prime$, with material density $\rho$ ($z^\prime$ is a dummy variable). Equivalently, the extra weight per vertical slice $dz$ is $dW=\rho\pi r(z)^2 dz$. We require that $\frac{W(z)}{\pi r(z)^2}$ is a constant stress $\sigma$.
What function solves $\frac{dr(z)}{dz}=\frac{\rho r(z)}{2\sigma}$? The exponential $r(z)\sim\exp\left(\frac{\rho z}{2\sigma}\right)$, and this provides an exponential/logarithm surface of revolution.
What does this have to do with algae growth? Assuming the algae is buoyant, upward movement is spontaneous, and thus we might expect vertical stringers of algae to form. But the vertical and bending stresses arising from gentle water motion could prompt proliferation in a mechanosensitive manner, in the same way that plants strengthen in the wind. Perhaps vertical assemblies of algae efficiently evolve to a stable level of constant stress, similar to our bones:
So the first hypothesis is that the algae features taper because of an intrinsic or externally imposed requirement for near-constant stress. This allows equations to be derived as described above. If the underlying biological behavior is confirmed and if the features are similar to the predictions, then we might be prepared to present an argument for causality, subject to strict and rigorous examination through experiment.
(2) Dendrite growth during solidification or precipitation
In a supersaturated solution or supercooled melt, protruding dendrites spontaneously form because any region that randomly pokes out a bit is exposed on more sides to material with a driving force to join it:


What does this have to do with algae growth? Algae that emerges slightly from the mat has more access to light and nutrients. The resulting spontaneous growth may always be upward due to buoyancy, but with accelerated growth and mounding around the source. (I don't know of a suitable constitutive equation, but the evolving shape could be numerically evaluated through kinetics simulations of light and nutrient absorption and growth.)
So the second hypothesis is that the tapered shape arises from instability-driven growth of randomly protruding algae.
(3) The deformation of an elastic membrane from a point force. (Thank you to @ChristopherJamesHuff for mentioning this in the comments.)
Waste gas from metabolic activity could collect under an algae mat and nudge it upward from buoyancy. Like the other two scenarios, this features positive feedback to draw out a tapered shape: Gas flows to the highest point, and so any random perturbation is unstable. The corresponding approximate (inverted) appearance is as follows, with the clamped boundary condition representing where the mat hasn't (yet) detached:
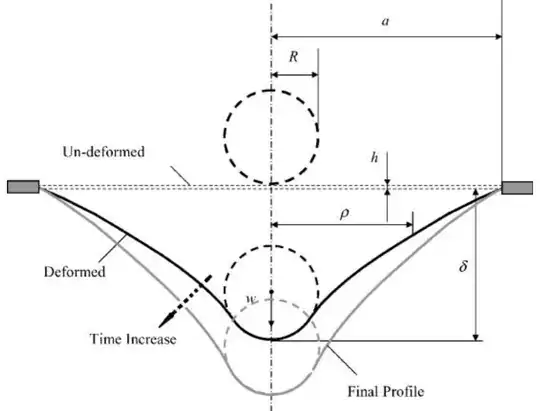
Although a closed-form equation may not exist for this shape due to the nonlinear nature of the mat elastically and permanently deforming (while proliferating), the process could be numerically simulated, as above.
The third hypothesis (contributed) is then that the tapered shape arises from gas-buoyancy-driven detachment and ascent of portions of the algae mat.
Now, one or more or none of these hypotheses may find experimental support. My point is that it's interesting to note that a shape in nature looks like a certain mathematical function, but it's arguably more rewarding to connect this—or another—equation with some reasonable biophysical justification.