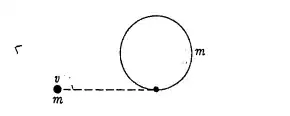
When using the conservation of angular momentum in collisions like the one in the following image.
Where there is a hoop of radius ${R}$ that is resting on a horizontal frictionless surface and a point particle of mass ${m}$ moving at a constant speed ${v}$. Considering an axis trough the center of mass of the hoop. If I wanted to calculate the angular momentum before the collision, using the conservation of angular momentum, because there are no external forces acting on the system, is the next relation valid? $\vec{L_i}$=${I}$$\vec{w_i}$=$\vec{L_f}$=${I}$$\vec{w_f}$, where ${I}$ is the moment of inertia, $\vec{L_i}$ the initial angular momentum (before collision) and $\vec{w_i}$ the initial angular velocity, $\vec{L_f}$ the final angular momentum (after collision) and $\vec{w_f}$ the final angular velocity. I tried calculating the initial angular momentum and I got $\vec{L_i}$=${mvr/2}$, where I used the relation I wrote before and i'm not sure whether thats right or wrong.