The criterion is that the derivative of Hamilton's action is zero.
The variation of the trial trajectory is variation of the spatial coordinate.
To find the point in variation space where the derivative of Hamilton's action is zero you take the derivative with respect to the variation. Since the variation is variation of position: you take the derivative of Hamilton's action with respect to the position coordinate.
(And of course, when there are multiple degrees of freedom you take the derivative for each of those spatial degrees of freedom.)
You want to populate the Euler-Lagrange equations with entities such that when you evaluate the Euler-Lagrange equation you will recover $F=ma$.
The operation that is specified/performed by the Euler-Lagrange equation is differentiation with respect to the position coordinate. Therefore in order to recover $F=ma$ you want to populate the equation with the integrals of the left hand side and the right hand side of $F=ma$
The integral of force with respect to the position coordinate gives the expression for potential energy.
About acceleration: in preparation for later use we take an arbitrary acceleration (an acceleration as a function of time), and integrate that with respect to the position coordinate.
In the following the differential is changed two times, the first change uses $ds = v \ dt$, the second change uses $a \ dt = dv$. With each change of differential the limits change accordingly.
$$ \int_{s_0}^s a \ ds = \int_{t_0}^t a \ v \ dt
= \int_{t_0}^t v \ a \ dt = \int_{v_0}^v v \ dv
= \tfrac{1}{2}v^2 - \tfrac{1}{2}v_0^2 \tag{1.1} $$
With the intermediate steps omitted:
$$ \int_{s_0}^s a \ ds = \tfrac{1}{2}v^2 - \tfrac{1}{2}v_0^2 \tag{1.2} $$
Incidentally, a remarkable property of (1.2) is this: the form of the right hand side is identical to the case of uniform acceleration.
With uniform acceleration:
$$ a (s - s_0) = \tfrac{1}{2}v^2 - \tfrac{1}{2}v_0^2 \tag{1.3} $$
So, how does it come about that (1.2) and (1.3) have identical right hand side? It goes back to the fact that position, velocity and acceleration are in a very special relation to each other. We have: position, first time derivative of position, second time derivative of position. Dimensionality; the product of acceleration and position has the same dimensionality as velocity squared. Those relations lead to special properties.
We take $F=ma$, and we integrate both sides with respect to the position coordinate:
$$ \int_{s_0}^s F \ ds = \int_{s_0}^s m \ a \ ds \tag{1.4} $$
Using (1.22) to develop the right hand side:
$$ \int_{s_0}^s F \ ds = \tfrac{1}{2}mv^2 - \tfrac{1}{2}mv_0^2 \tag{1.5} $$
(1.5) is the Work-Energy theorem.
The way that potential energy is defined slots in with the left hand side of (1.5), and the way that kinetic energy is defined slots in with the right hand side of (1.5)
As we know: the following is the operation that the Euler-Lagrange equation performs on the kinetic energy:
$$ \frac{d}{dt} \left( \frac{d(\tfrac{1}{2}mv^2)}{dv} \right) = \frac{d}{dt} (mv) = ma \tag{1.6} $$
It looks as if (1.6) does something other than taking the derivative with respect to the position coordinate, but that is actually not the case.
$$ \frac{d(\tfrac{1}{2}mv^2)}{ds} = \tfrac{1}{2}m\left( 2v\frac{dv}{ds} \right) = m\frac{ds}{dt}\frac{dv}{ds} = m\frac{dv}{dt} = ma \tag{1.7} $$
(1.6) and (1.7) evaluate to the same quantity: $ma$, the product of mass and acceleration. That means that (1.6) and (1.7) are in fact the same differentiation, only different notation.
There are also classes of cases such that the true trajectory corresponds to a maximum of Hamilton's action. Example: when the potential energy increases in proportion to the cube of the displacement: the true trajectory is at a point in variation space such that Hamilton's action is at a maximum.
It is essential to not think in terms of minimum or maximum. It is clear that minimum/maximum is immaterial. What counts is the derivative of Hamilton's action.
When the rate of change of kinetic energy matches the rate of change of potential energy everywhere along the trajectory: that is the true trajectory.
The point in variation space where those two rates of change match each other everywhere is the point in variation space where the derivative of Hamilton's action is zero.
In the following I expand on the 'derivative is zero' criterion.
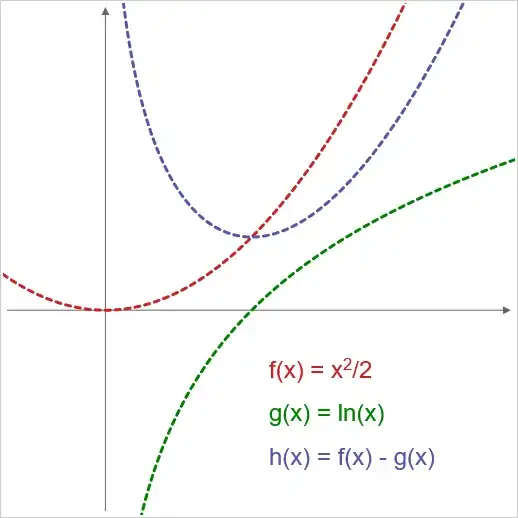
In the diagram red curve and the green curve are both ascending functions.
Red: $f(x) = \frac{1}{2} x^2$
Green: $ g(x) = ln(x) $
Problem: at what x-coordinate do the functions $f(x)$ and $g(x)$ have the same slope?
Phrased differently: at what x-coordinate is the rate of change of $f(x)$ equal to the rate of change of $g(x)$?
The direct way to answer that question is to start by taking the derivative of each function, and then solve for the point where the two derivatives have the same value:
$$ \frac{f(x)}{dx} = \frac{g(x)}{dx} \tag{2.1} $$
$$ \frac{\tfrac{1}{2}x^2}{dx} = \frac{ln(x)}{dx} \tag{2.2} $$
$$ x = \frac{1}{x} \tag{2.3} $$
There is also a more convoluted way to address the problem:
I will refer to this more convoluted way as constructing a 'mathematical action':
Create a third function by subtracting the second function from the first function.
$$ h(x) = f(x) - g(x) \tag{2.4} $$
$$ h(x) = \tfrac{1}{2} x^2 - ln(x) \tag{2.5} $$
In the diagram the blue curve represents $h(x)$, the 'mathematical action'.
The point where the derivative of the blue curve, the 'mathematical action', is zero, is the point where the red curve and the green curve have the same slope, the same rate of change.
In the case of application of the Euler-Lagrange equation: we can think of the true trajectory as subdivided into a concatenation of infinitesimally short subsections. Hamilton's action has a derivative of zero if and only if along each infinitesimal subsection the rate of change of kinetic energy matches the rate of change of potential energy.
