It is been said that KVL follows law of conservation of energy. But I'm not getting the analogy between them. How does KVL supports law of conservation of ENERGY?
6 Answers
Within the limitations pointed out in the answer by @naturallyinconsistent), KVL follows the law of conservation of energy in that the electrical potential energy supplied per unit charge in a circuit by voltage sources equals the energy that is either dissipated or stored per unit charge in the circuit resistance, capacitance, and inductance. Or, as it is often stated, the sum of the voltage rises (energy supplied) equals the sum of the voltage drops (energy dissipated or stored) in a circuit.
Hope this helps.
- 81,786
KVL has nothing to do, conceptually, with conservation of energy.
KVL is a rule relating electric potential drops on circuit elements in any closed loop in a circuit: because potential is a single-valued function of position, in general, sum of potential drops on elements in a closed path is always zero.
True, this means electric potential energy of a charge returns to the original value after the charge returns to the original position. So, potential energy of single travelling charge changes in time, but repeatedly returns to some previous value, when the charge returns to previous position.
But this does not mean conservation of electric potential energy in time, or conservation of all energy in time. Electric potential energy of travelling charge decreases as it moves along in the circuit, and increases in the battery, or power source. Also, EM energy is typically not conserved, even while KVL holds; for example, in a circuit where current flows through resistors, some EM energy is transformed into heat. KVL is valid, but EM energy is dissipated into other forms.
- 44,745
Voltage is defined as the energy per charge moved across the voltage difference. In a conservative situation, when you move the charge around in a loop and go back to where you are, it should be obvious that the potential energy of the charge goes back to what it was before, and hence it is a statement of the conservation of energy.
Note that, strictly speaking, this has to be done quasistatically, because an accelerating charge radiates energy away in the form of light.
Note also that it is a special case to consider conservative situation here. KVL is the special case of Faraday's Law, and when you are no longer in the conservative situation, Faraday's Law tells you how much the energy will not be conserved. It is not conserved because it is going to be taking or giving away energy into the electromagnetic field, which encompasses the situation I just covered earlier.
- 14,919
I wanted to give a mathematical answer as I believe it illustrates the point quite clearly. The Kirchoff's loop law directly follows from Maxwell's Equations. Consider the following Maxwell equation:
$$ \nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}$$
If you are unfamiliar with the notation, this just means that a changing magnetic field produces an electric field that likes to curl. Now consider a loop in your circuit and integrate both sides on the surface the loop covers. We then have
$$ \int_ S (\nabla \times \vec{E}) \cdot d\vec{A} = \int_ S \frac{\partial \vec{B}}{\partial t} \cdot d\vec{A}$$
Now if we have a simple circuit with a steady current, the magnetic field will be 0 $\vec{B} = 0$. So our equation becomes
$$ \int_ S (\nabla \times \vec{E}) \cdot d\vec{A} = 0$$
We can now use Stokes's theorem to change this surface integral to a line integral and we have
$$ \int_{Loop} \vec{E} \cdot d\vec{l} = 0$$
Remembering that the voltage is defined as $\Delta V_{AB} = -\int_{A}^B \vec{E} \cdot d\vec{l}$, we deduce that in the circuit $\Delta V$ = 0, i.e the total potential difference must be 0. This can be interpreted as energy conservation as the fact that there is no varying magnetic field (and therefore a varying electric field), the system cannot gain any energy from the electromagnetic fields. What must go in also must come out.
- 1,814
To amplify on @JanLalinsky's answer, KVL and KCL are not really physics but is a topological result on linear graphs that allows us a consistent set of labeling (numbering) of nodes and branches, see BAMBERG & STERNBERG : A COURSE IN MATHEMATICS FOR STUDENTS OF PHYSICS, chapter 12. This topological content is expressed in Tellegen's theorem that is a rather surprising generalization of energy conservation itself. Physics comes in by our ability to separate the electromagnetic energetic phenomena into spatially distinct pieces of electric energy, magnetic energy, and dissipated energy and assign them to the branches of the graph. Once you place those numerical values on the graph (network) energy conservation, and more, is assured.
- 21,193
The potential difference between to positions $A$ and $B$ is minus the work done by an electric field $\vec E$ in taking unit positive charge between those two positions.
$V_{\rm AB}= -\displaystyle \int_{\rm A}^{\rm B} \vec E \cdot d\vec \ell$
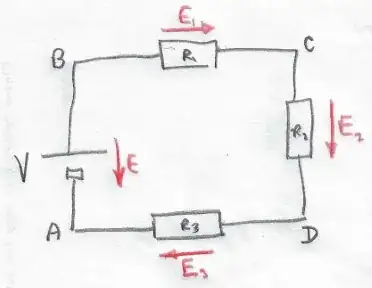
So consider the following circuit with unit positive charge completing the loop $ABCDA$.
Work done by electric field in moving unit positive charge from:
A to B
$V_{\rm AB}= -\displaystyle \int_{\rm A}^{\rm B} \vec E \cdot d\vec \ell$
The integral will have a negative value as the directions $\vec E$ and $\vec d\ell$ are opposite and so $V_{\rm AB}$ will be positive. Put another way there is an external force (due to an electrochemical reaction) which is doing positive work in moving the unit positive charge from $A$ to $B$.
The next three integrals will have a positive value as $\vec E$ and $\vec d\ell$ are in the same direction and so each of the three potential differences will be negative.
B to C
$V_{\rm BC}= -\displaystyle \int_{\rm B}^{\rm C} \vec E_1 \cdot d\vec \ell$
C to D
$V_{\rm CD}= -\displaystyle \int_{\rm C}^{\rm D} \vec E_2 \cdot d\vec \ell$
D to A
$V_{\rm DA}= -\displaystyle \int_{\rm D}^{\rm A} \vec E_3 \cdot d\vec \ell$
For the complete loop the net work done by the electric fields is zero, ie
$V_{\rm AB}+V_{\rm BC}+V_{\rm CD}+V_{\rm DA}=0$
which is Kirchhoff's voltage law.
The analysis above assumes that there is no magnetic change linked with the circuit.
- 104,498