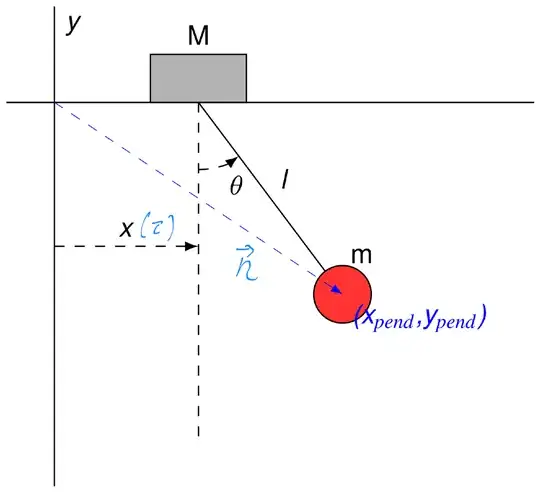
Take a simple example like the pendulum with a moving support (But only considering the pendulum mass $m$, not the support mass $M$): https://en.wikipedia.org/wiki/Lagrangian_mechanics#/media/File:PendulumWithMovableSupport.svg
From my understanding I could formulate the Lagrangian for the moving reference frame from the perspective of an observer sitting on the support. Using the pendulum angle $\theta$ as the only coordinate and considering only the velocity relative to the moving reference frame. $r$ is the length of the pendulum. With $L=T-V$ ($T$ for kinetic, $V$ for potential energy, $Q$ for generalized forces not included in the energy) I end up with:
$$ \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial L}{\partial \dot{\theta}} - \frac{\partial L}{\partial \theta} - Q = m r^2 \ddot{\theta} + m g r \sin \theta - Q = 0 $$ With the acceleration of the frame $\ddot{x}$ and the position vector of m, $\mathbf{r}$ I can add the only additional force: $$ Q = \frac{\partial \mathbf{r}}{\partial \theta} \cdot \ddot{x} (-1, 0) = - m \ddot{x} r \cos \theta $$ So I can eliminate $m$ and $r$ and get: $$ r \ddot{\theta} + g \sin \theta + \ddot{x} \cos \theta = 0 $$ Which is the same solution as wikipedia gives for the moving pendulum.
So far, all examples I've seen considered a moving reference frame by adding the relative speed to an inertial reference frame in the system's kinetic energy. As I understand it, I can just as well look at all movements relative to the moving frame and view the acceleration from 'outside' as an extra force. Which in some cases might make the algebraic stuff easier, I think.
Am I just lucky in this case and making wrong assumptions or is this a valid way to get to the equations of motion?