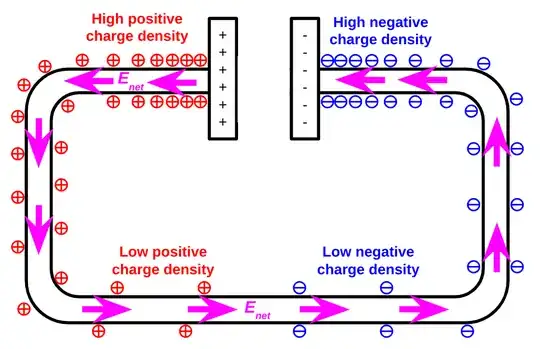
we know that in a simple circuit (a battery and a resistor) the battery induces surface charges on the surface of the wire such that the net electric field due to battery+surface charges inside the wire is constant and is directed along the axis of the wire and the current starts flowing. We know that these surface charges also have some field which it exerts on the battery which is balanced by the internal mechanism of the battery to make sure that there is a constant potential difference across the battery ends.
But if we consider the scenario of a capacitor+resistor (discharging), then the surface charges must also exert some field between the plates of the capacitor, this must change the field strength between the plates, hence changing the formula of $E=σ/2ε$ to something different, So even the $∆V$ changes to a different value. But why do we ignore this effect and just use the formula $∆V=σd/2ε$?
This answer explains why it is for the battery https://physics.stackexchange.com/a/108157/370982 but doesn't touch upon capacitors. Even the book "Matter and interactions" doesn't explain this issue, so looking forward to answers.