2

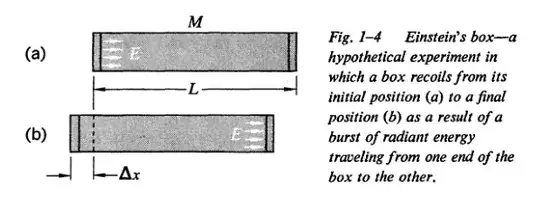
In French, Special Relativity, pg. 16-17, the 'Einstein's box' thought experiment is explained. It starts with a box of length $L$, mass $M$ and we emit photons from one end that have energy $E$. Then it's argued that the box moves opposite to the direction of the photons by an amount $\Delta x = \frac{E L}{M c^2}$. And then, since we suppose it's an isolated system, we say that the center of mass hasn't moved and argue that the photons must have carried some mass $m$ with them. My problem is that I can't make sense of the calculation for this center of mass. Here's the picture from the book.

We fix the origin at the left end of the box. At (a) the center of mass is in $L/2$. In (b) we have the box of mass $M-m$ that is centered at $L/2 -\Delta x$ and the photons of mass $m$ that have reached $L-\Delta x$. So the center of mass in (b) will be in

$$ (M-m) (L/2-\Delta x)+m(L-\Delta x)$$

all over the total mass $M$. Equating this with the center of mass in (a) gives $$m = \frac{2 M \Delta x}{L}$$ which is a factor of two off the correct result. Where am I wrong?

blundered_bishop
  • 145
  • 4

1 Answers1

3

As @mmesser314 points out, you've made a little mistake in your setup. You say that

We fix the origin at the left end of the box. At (a) the center of mass is in $L/2$.

But then, this second sentence would only be true if the center-of-mass for the box without the photons $(M-m)$ were at $L/2$ and the photons were at the center of the box, $L/2$. That is, if the photons only had to travel half as far as you actually intend for them to travel. Not coincidentally, the value for $\Delta x$ that you've calculated is only half as much as the expected result.

If, instead, the photons are at $0$ initially, then the actual center of mass at (a) is \begin{equation} \frac{M-m}{M}\frac{L}{2} + \frac{m}{M}\, 0 = \frac{M-m}{M}\frac{L}{2}. \end{equation} Now, equate this to your result for (b), and it works out to the same thing as French got: \begin{equation} \frac{M-m}{M}\frac{L}{2} = \frac{M-m}{M} \left( \frac{L}{2} - \Delta x \right) + \frac{m}{M} \left( L - \Delta x \right). \end{equation} This simplifies to \begin{equation} \Delta x = \frac{m L}{M} = \frac{E L}{M c^2}, \end{equation} as expected.

It's worth noting that French's derivation was in terms of momenta and speeds, so it's very good of you to try to derive the result in a different way. Nice work!

Mike
  • 15,586