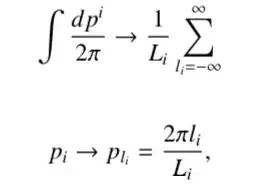How to "naively" calculate the vacuum energy density in a $4 + d$ spacetime?

Question

The "naive" calculation of the vacuum energy density in flat 4D spacetime is resumed by the following divergent integral (I'm considering only free massless fields): $$\tag{1} \rho_{\text{vac}} = \int_0^{\infty} \frac{1}{2} \, \hbar \omega \, \frac{d^3 k}{(2 \pi)^3}. $$ Very frequently, authors are introducing some Lorentz breaking cut-off frequency $\omega_{\text{max}}$ to get a finite result. So for the open infinite 3D flat space: $$\tag{2} \rho_{\text{vac}} = \frac{\hbar}{2 (2 \pi)^3} \int_0^{\omega_{\text{max}}} \omega^3 \, 4 \pi \, d\omega = \frac{4 \pi \hbar}{2 (2 \pi)^3} \, \frac{\omega_{\text{max}}^4}{4}. $$ This is all well known. Now, I want to consider some $3 + d$ dimensional extension of this calculation. Consider a flat space of 3 open infinite dimensions + $d$ "internal" (i.e finite closed) dimensions, of spacetime metric $$\tag{3} ds^2 = dt^2 - (dx^2 + dy^2 + dz^2) - b^2 (d\theta_1^2 + d\theta_2^2 + \dots + d\theta_d^2), $$ where $x$, $y$ and $z$ are the usual cartesian coordinates in the open 3D space, while $0 \le \theta_i < 2 \pi$ ($i = 1, 2, \dots d$) are finite angular coordinates in the $d$ dimensional extension. $b$ is a constant (the "radius" of the internal dimensions). Note that I put $c \equiv 1$ for simplicity and I'm using the $\eta = (1, -1, -1, ...)$ metric signature. The spacetime described by metric (3) can be thought as a flat $d$-torus joined to the usual 4D Minkowski spacetime.

Many authors are considering a trivial $D$ dimensional extension of (1)-(2), but this isn't exactly what I'm interested in, since it implies an open $D$-euclidian space (here, $D$ would be $3 + d$): $$\tag{4} \rho_D = \int_0^{\omega_{\text{max}}} \frac{1}{2} \, \hbar \omega \, \frac{d^D k}{(2 \pi)^D} \propto \int_0^{\omega_{\text{max}}} \omega^D \, d\omega \: \Omega_D = \frac{\omega_{\text{max}}^{D + 1}}{D + 1} \: \Omega_D, $$ where $\Omega_D$ is the "solid angle" in $D$ dimensional euclidian space, such that $\Omega_3 = 4 \pi$ for $d = 0$ (i.e $D = 3$).

So my question is how should we change (1)-(2), if the extended $D = 3 + d$ space contains a closed, flat compact $d$ dimensional extension? Would it be right to simply use the following formal substitutions? $$\tag{5} d^3 k \quad \Rightarrow \quad d^3 k \, dq_1 \, dq_2 \dots dq_d, $$ and $$\tag{6} \omega = || \mathbf{k} || =?\!=\, \sqrt{k_x^2 + k_y^2 + k_z^2 + q_1^2 + q_2^2 + \dots + q_d^2} \,. $$ But then, what should be the integration domain for the $q_i$ momentum variables in the closed flat-torus space? I'm expecting some discrete values, that could be extended to a continuous interval since the integral is still divergent and would get most of its contribution from very high momentum modes. What would be the equivalent of the "solid angle" $\Omega_D$ in such a universe? $\Omega_D = 4 \pi (2\pi)^d$ ??

---

EDIT: For reference, the solid angle in an open euclidian $D$ dimensional space is $$\tag{7} \Omega_D = \frac{2 \sqrt{\pi}^D}{\Gamma(D/2)}. $$ This formula gives $\Omega_1 = 2$, $\Omega_2 = 2\pi$, $\Omega_3 = 4 \pi$, $\Omega_4 = 2 \pi^2$, etc.

Answer 1

$\newcommand{\d}{\mathrm{d}}\newcommand{\R}{\mathbb{R}}\newcommand{\T}{\mathbb{T}}\newcommand{\norm}[1]{\left\Vert#1\right\Vert}\newcommand{\L}{\mathbb{L}}$So, the setup we are interested in is the following. We have a free massless scalar on $\R\times\R^n\times \T^{D-n-1}$, where the first $\R$ factor indicates time and $\T^{D-n-1}$ is a $(D-n-1)$-torus. I will denote as $k,p,$ and $\xi$ the momenta o the full spacetime, on $\R^n$ and on $\T^{D-n-1}$ respectively. You can think of the most general $(D-n-1)$-torus as a quotient of $\R^{D-n-1}$ by a full-rank, integer lattice $\L$. For instance the rectangular torus with radii $\{R_1,R_2,\cdots R_{D-n-1}\}$, is associated with the lattice $$\L = \frac{2\pi}{R_1}\mathbb{Z}\oplus \frac{2\pi}{R_2}\mathbb{Z} \oplus \cdots \frac{2\pi}{R_{D-n-1}}\mathbb{Z}.\tag{1}$$ This makes it clear, that the eigenvalues of the operator $\xi\in\L$. This is just a rephrasing of what you said, that momenta in the compact directions are quantised.

The vacuum energy density is then $$\rho = \int_{\R^n\times \T^{D-n-1}} \d\mu(k) \omega(k),$$ where $\d\mu(k)$ is a measure, to be specified later on, and $$\omega(k) = \sqrt{\norm{k}^2} = \sqrt{\norm{p}^2+\norm{\xi}^2}.$$ The measure is simply flat along the noncompact directions and counting along the compact directions, i.e. $$\rho = \operatorname{covol}(\L)\sum_{\xi\in\L}\int_{\R^n} \frac{\d^n p}{(2\pi)^n} \sqrt{\norm{p}^2+\norm{\xi}^2},$$ where $\operatorname{covol}(\L)$ is the covolume of the lattice, which is there to account for the correct dimensionality of the vacuum energy density, i.e. $[\rho] = \text{energy}/{\text{volume}_{D-1}}= \text{energy}^{1+n+(D-n-1)} = \text{energy}^{D}$. In the case of the exemplary rectangular lattice, (1), $$\operatorname{covol}(\L) = \prod_{i=1}^{D-n-1}\frac{2\pi}{R_i}.$$

Now, as you can see from the above example there is a zero mode, i.e. a mode with zero momentum along the torus. This we must separate, i.e. we split $\L$ as $\L=(0,0,\cdots,0)\cup\L'$, where $\L':=\L\setminus(0,0,\cdots,0)$. So the vacuum energy becomes: $$\rho = \int \frac{\d^n p}{(2\pi)^n} \sqrt{\norm{p}^2} + \sum_{\xi\in\L'}\int_{\R^n} \frac{\d^n p}{(2\pi)^n} \sqrt{\norm{p}^2+\norm{\xi}^2}.$$ The first summand is just the vacuum energy density of a massless particle and the second one is the energy density of an infinite tower of massive particles. This you can now easily integrate by going to polar coordinates $$\d^n p = \d\norm{p} \d\Omega_n \norm{p}^{n-1}.$$ Of course it will diverge, but we will integrate up to a cutoff, $\Lambda$, getting: $$\int_{\R^n}^{\norm{p}^2<\Lambda} \frac{\d^n p}{(2\pi)^n} \norm{p} = \frac{\Omega_n}{(2\pi)^n}\frac{\Lambda^{n+1}}{n+1},$$ and $$ \int_{\R^n}^{\norm{p}^2<\Lambda} \frac{\d^n p}{(2\pi)^n} \sqrt{\norm{p}^2+\norm{\xi}^2} = \frac{\Omega_n}{(2\pi)^n}\frac{\Lambda^{n}\norm{\xi}}{n}\ {}_2F_1\left(-\frac{1}{2},\frac{n}{2};\frac{2+n}{2};-\frac{\Lambda^2}{\norm{\xi}^2}\right),$$ where $\Omega_n$ is the volume of the $n$-sphere $$\Omega_n = \frac{2\pi^{n/2}}{\Gamma\!\left(\frac{n}{2}\right)},$$ and ${}_2F_1(a,b;c;z)$ is the ${}_2F_1$ hypergeometric function.

In total then, the regularised vacuum energy density is $$\rho_\Lambda = \operatorname{covol}(\L)\frac{\Omega_n\Lambda^{n}}{(2\pi)^n}\left[ \frac{\Lambda}{n+1} + \frac{1}{n}\sum_{\xi\in\L'}\norm{\xi}\ {}_2F_1\left(-\frac{1}{2},\frac{n}{2};\frac{2+n}{2};-\frac{\Lambda^2}{\norm{\xi}^2}\right)\right].$$

Specialising to $n=3$, which was your original question, the hypergeometric function simplifies and you get you get $$\rho_\Lambda = \operatorname{covol}(\L)\frac{\Lambda^{3}}{2\pi^2}\Bigg[\frac{\Lambda}{4} + \\ \frac{1}{24}\sum_{\xi\in\L'}\norm{\xi}\left(\Lambda^{-2}\sqrt{1+\frac{\Lambda^2}{\norm{\xi}^2}}\left(2\Lambda^2+\norm{\xi}^2\right)-\frac{\norm{\xi}^3}{\Lambda^3}\operatorname{arcsinh}\!\left(\frac{\Lambda}{\norm{\xi}}\right)\right)\Bigg].$$

Note a few key features of the above construction:

• The vacuum energy density is UV divergent. That is of course to be expected, cf. this physics.SE answer

• The vacuum energy density is also divergent from the sum over non-zero $\xi$. That is because by compactifying you got a whole infinite tower of massive particles of ever increasing mass. That lies in the heart of Kaluza-Klein reduction and more generally string compactifications

• The solid angle only comes in in the non-compact directions. In this case, when $n=3$ which is your original question you only see $\Omega_3$. This is because on the torus there is only one mode with zero momentum. In general, if you compactify on another manifold, (replace $\mathbb{T}^{D-n-1}$ with a compact manifold $S_{D-n-1}$) which has a moduli space of zero-modes, i.e. a manifold, $\mathcal{M}:=\left\{\xi\in S_{D-n-1}^\vee\vert \xi=0\right\},$ where $S_{D-n-1}^\vee$ is the formal "momentum space" associated to $S_{D-n-1}$, then you would get a contribution from the massless modes to the vacuum energy: $$\rho_\Lambda^{\xi=0} = \operatorname{covol}(\L)\frac{\Omega_n}{(2\pi)^n}\frac{\Lambda^{n+1}}{n+1}\operatorname{vol}(\mathcal{M}).$$

Answer 2

Having the D-Torus as part of the topology means you have to discretize the new momentum variables.

As the field you are considering is a massless bosonic one, this means to take the following substitutions for every compactified dimension in the integral:

Where L_i is the length of the i-th extra spatial dimension (in your case this is equal to "b" for every "i"). Computing the resulting integral is non-trivial and probably won't give you a straightforward solid angle generalization.

A general result for the bosonic propagator can be still be obtained tough, you can refer to page 14 of the following publication: https://arxiv.org/pdf/1409.1245.pdf

from there you can build the feynman rules and in theory get to the vacuum energy. As this energy is closely related to studying the casimir effect of such fields, this publication might also prove useful to you: https://arxiv.org/pdf/1608.01367.pdf

The author sheds some light on the vacuum energy computation via Zeta function regularizations.