How do electrons from a battery move through a circuit?

Question

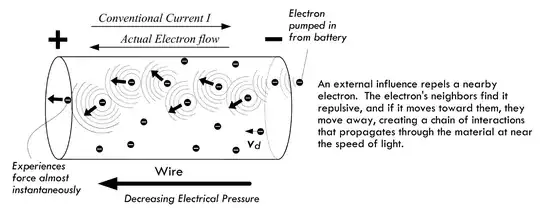
I'm reading a book called Practical Electronics for Inventors and it describes the method by which batteries generate electron flow as follows: the battery releases a few electrons via a chemical reaction; the free electrons floating in the wire adjacent to the anode are repelled by these additional electrons, so they shove the free electrons adjacent to them and this process continues all the way to end of the wire near the cathode.

The book then says

"It is likely that those electrons farther “down in” the circuit will not feel the same level of repulsive force, since there may be quite a bit of material in the way which absorbs some of the repulsive energy flow emanating from the negative terminal (absorbing via electron-electron collisions, free electron–bond electron interactions, etc.)."

The book is essentially describing voltage as the relative capacity to "shove" adjacent electrons and it says the electrons near the cathode feel the least "shove" because throughout the circuit electrons have been colliding with other things.

I understand how this explains resistance when an actual load is placed in a circuit (LED, resistor, etc). But what if you connected the ends of a battery with a wire? Will the free electrons in the wire near the cathode feel the least "shove" because the "shoving force" diminishes due to electrons colliding with the wire walls? Or is this effect marginal in wires, so free electrons near the cathode are equally capable of shoving as the ones near the anode? The reason this confuses me is because one can obviously connect a multimeter across a battery to measure its voltage, but doesn't that imply there's a difference in shove between electrons at the ends despite the lack of a load?

Answer 1

The book explanation is somewhat misleading but your suggestion of a wire connecting the two terminals of an ideal battery is a good one.

A complex electrochemical reaction within the battery sets up and maintains a constant potential difference across the terminals of the battery with an excess of electrons on the negative terminal and a deficit of electrons on the positive terminal.
That reservoir of changes on the terminals is kept replenished by the electrochemical reaction inside the battery.

When a wire is connected across the terminals of the battery an electric field is produced by the charges on the battery terminals and that electric field accelerates (gives kinetic energy) to the mobile electrons in the wire.
However the mobile electrons collide with the lattice ions in the wire and in doing so give some of their kinetic energy to the lattice ions which as a consequence vibrate more (are at a higher temperature).
As a consequence of the repeated acceleration and interaction with the lattice ions of the mobile electrons those mobile electrons move at a constant average velocity throughout the wire (drift velocity), ie there is no slowing down of the drift velocity). If you could observe the mobile electrons you could not distinguish between their motion at any position along the wire, ie there is no less "shove" near one of the terminals as compared with the "shove" near the other terminal.

If the conductors between the terminals of the battery were non-uniform, ie wires and resistors, then the current (charge passing a point per unit time) through each of the elements of the circuit would be the same but the potential difference across each of the components would differ, it being larger across components with larger resistance.
What this means is that the electric field has to do more work driving the mobile charge through higher resistance components, ie the potential difference is higher.

As a final point, the mobile electrons just circulated around the circuit under the influence of the electrochemical reaction within the battery which is the reason for the separation of positive and negative charges. The simple model of water (mobile charges) circulating around a closed loop which includes a pump (battery) is not a bad one.