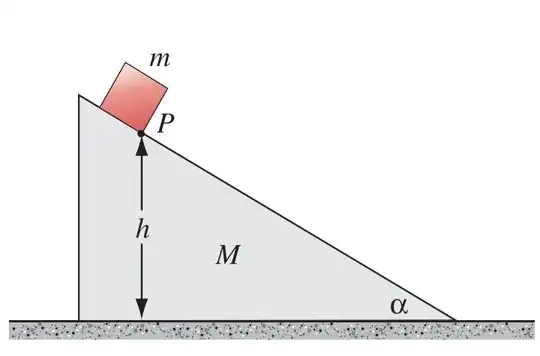
Recently I was solving a problem involving a block on triangular wedge kept on horizontal fricitionless surface and the system is released from rest. All things are indicated in figure,
Now I am finding final velocities of blocks after block reaches ground using several methods.
$N$ represents normal between wedge and block and $N_s$ represents the normal between wedge and surface, $x_1$ represents horizontal displacement of $m$, $x_2$ represents horizontal displacement of $M$, $v_1$ & $v_2$ are final velocities of $m$ & $M$ respectively.
Appling work energy theorem :
$$\begin{align} N\cos\alpha\cdot x_1+(mg-N\sin\alpha)\cdot h+N\cos\alpha\cdot x_2+(N_s-N\sin\alpha)\cdot 0+Mg\cdot 0= \frac{mv_1^2}{2}+ \frac{Mv_2^2}{2} -0 \end{align}$$
Rearranging this gives,
\begin{equation}\tag{1} mgh+N((x_1+x_2)\cos\alpha-h\sin\alpha)=\frac{mv_1^2}{2}+ \frac{Mv_2^2}{2}\end{equation}
Conservation of energy of center of mass :
$$\tag{2} mgh=\frac{mv_1^2}{2}+ \frac{Mv_2^2}{2}$$
By $(1)$ and $(2)$
$$N((x_1+x_2)\cos\alpha-h\sin\alpha)=0$$
So, this gives me that work done by normal is zero. But this was mathematics not physics.
What is exactly workdone by normal force?
Since point of contact changes every time as the block goes down, simply there is not a single particle which exerts normal on the other particle of block.
And can you tell me why this thing comes to be zero?
In the other words,
Why is the workdone by normal on wedge is of opposite sign and equal in magnitude to that of workdone by normal on block?
Please try to use mathematics as less as possible