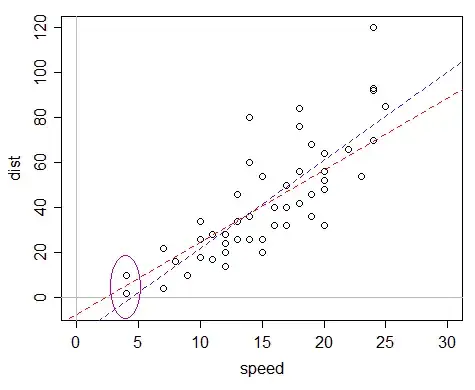
You should almost always include the intercept. Not including the intercept can lead to bias in your estimate of the slope in your model as well as other problems.
it is generally a safe practice not to use regression-through-the origin model and instead use the intercept regression model. If the regression line does go through the origin, b0 with the intercept model will differ from 0 only by a small sampling error, and unless the sample size is very small use of the intercept regression model has no disadvantages of any consequence. If the regression line does not go through the origin, use of the intercept regression model will avoid potentially serious difficulties resulting from forcing the regression line through the origin when this is not appropriate.
(Kutner, et al. Applied Linear Statistical Models. 2005. McGraw-Hill Irwin).
This I think summarizes my view on the topic completely.
Other cautionary notes include:
Even if the response variable is theoretically zero when the predictor variable is, this does not necessarily mean that the no-intercept model is appropriate
(Gunst. Regression Analysis and its Application: A Data-Oriented Approach. 2018. Routledge)
It is relatively easy to misuse the no intercept model
(Montgomery, et al. Introduction to Linear Regression. 2015. Wiley)
regression through the origin will bias the results
(Lefkovitch. The study of population growth in organisms grouped by stages. 1965. Biometrics)
in the no-intercept model the sum of the residuals is not necessarily zero
(Rawlings. Applied Regression Analysis: A Research Tool. 2001. Springer).
Caution in the use of the model is advised
(Hahn. Fitting Regression Models with No Intercept Term. 1977. J. Qual. Tech.)
To explore this in a little more depth let's suppose that our data follows the equation $$y=\beta_1 x + \beta_0 + \mathcal{N}(0,\sigma)$$ where for concreteness $\beta_0=6$ and $\sigma=5$. Suppose also that we have a good scientific theoretical model that says $\beta_0 = 0$. Let's see what happens if we fit our data to 3 different models:
- An "overfitted" quadratic model: $y=\beta_2 x^2 + \beta_1 x + \beta_0 $
- The recommended "intercept" model: $y=\beta_1 x + \beta_0$
- The theoretical "no-intercept" model: $y=\beta_1 x$
Let's sample 21 data points as follows:

Now, visually it seems that for $\beta_1=1$ and $\beta_0=6$ and $\sigma=5$ the small intercept is negligible, and the theoretical no-intercept model should be fine to use. The no-intercept model has an estimated $\beta_1 = 1.100 \ [1.044,1.157]$ which confidently excludes the true value of $1$. In contrast, the intercept model has an estimated $\beta_1 = 0.944 \ [0.874, 1.014]$ and the quadratic model has $\beta_1 = 1.091 \ [0.825, 1.358]$, both of which include the true value in the 95% confidence interval.
If we repeat this 1000 times we obtain the following histogram:

The intercept model is the best of these three, with the no-intercept model missing the true parameter in its confidence interval and the quadratic model having an overly broad confidence interval. This is confirmed by the Bayesian information criterion (BIC) which is lowest for the intercept model.
So one danger of the no-intercept model is the tendency to artificially introduce bias into the slope.
Another issue is the tendency to produce a statistically significant result even when there is no trend. To investigate this we will generate data with $\beta_1=0$ and $\beta_0=6$.
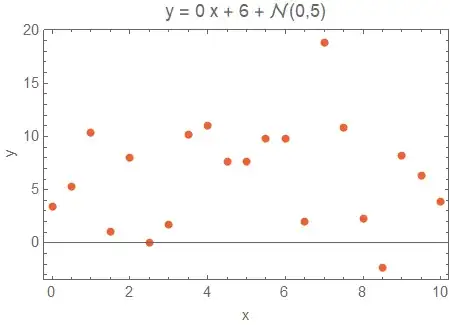
In this case the no-intercept model hallucinates a slope of $\beta_1=0.974 \ [0.521,1.428]$. Not only does this model invent a non-existent effect, it is quite confident, with a highly significant p-value of $p<0.001$, that the effect is non-zero. In contrast the intercept model obtains a non-significant ($p=0.792$) slope of $\beta_1 = 0.097 \ [-0.658,0.852]$, and the quadratic model obtains $\beta_1 = 1.892 \ [-0.951,4.735]$.
Again, repeating 1000 times we obtain

Again, the intercept model is the best of these three, with the no-intercept model missing the true parameter in its confidence interval and the quadratic model having an overly broad confidence interval. This is confirmed by the BIC which is again lowest for the intercept model.
So another danger of the no-intercept model is the tendency to artificially invent effects that do not exist, and to falsely produce such effects with a high degree of confidence.
Finally, let's examine the behavior of these models in the situation where the no-intercept model is actually appropriate. Here we will set $\beta_1=1$ and $\beta_0=0$ so the data actually matches the theoretical no-intercept model.
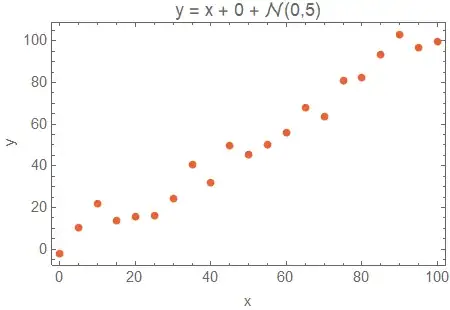
In this case all three models include the true slope of $1$ in the confidence interval. The no-intercept model estimates $\beta_1 = 1.021 \ [0.972,1.069]$ while the intercept model estimates $\beta_1 = 1.043 \ [0.947,1.139]$ and the quadratic model estimates $\beta_1 = 0.768 \ [0.415, 1.120]$.
Repeating this 1000 times we obtain the histogram:
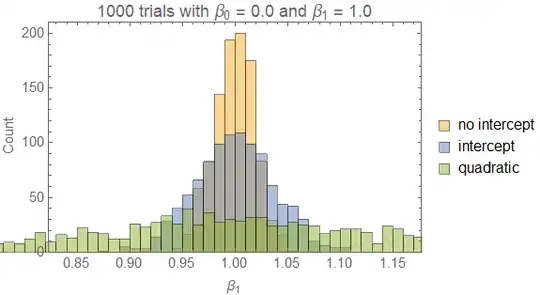
This time, the no-intercept model is slightly better. All models provide an unbiased estimate of the $\beta_1$ parameter, but the no-intercept model has a slightly more narrow confidence interval. This is reflected in the fact that the no-intercept model has the lowest BIC of the three.
So, if a no-intercept model is desired, then an appropriate procedure would be to fit an intercept model, check the intercept, if it is not significant then fit the no-intercept model, and use some model-selection criterion to choose. But the first step will necessarily be to fit an intercept model. And often the extra steps are not worth the small improvement in precision gained with the no-intercept model.