If I've understood things right, light cannot escape from inside the event horizon. So let's say that I'm falling into a black hole, and I'm looking at my feet. At some point, my head will be outside of the event horizon, but my feet will be inside. Does this mean that I can no longer see my feet, since the light reflected from them can't reach my eyes?
Asked
Active
Viewed 332 times
2 Answers
4
Assuming the black hole is large (so we don't have to worry about tidal forces), you could see your feet without any issue. Due to the equivalence principle, physics are no different as you cross the event horizon as they are anywhere else.
The light from your feet doesn't escape the event horizon to reach your eyes, though. Locally, the horizon moves outward at the speed of light. (Think of how outward-moving light can be trapped on the horizon.) Since the light from your feet doesn't move faster than light, it isn't going to pass the horizon.
Sten
- 7,910
3
I love this question. You probably imagine the Event Horizon as a sphere of darkness sitting in space. Once you plunge into it, your feet suddenly disappear, because they are now inside the event horizon while your head is outside, so the light reflected from your feet can't reach your head. Is this the correct way to think about it? Not quite.
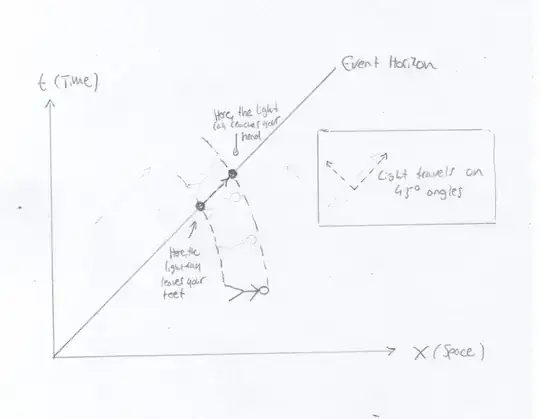
The problem is, you are thinking about the situation in a non-relativistic way. The whole point of special relativity is that time and space are not distinct concepts. They form a single entity called space-time. So you have to imagine the event horizon as an object that exists both in space and in time. This gets confusing very quickly, because our brains are not evolved to think relativistically. It helps to consider the situation in what is called a space-time diagram. They are incredible helpful for solving problems like this.
It is enough to consider the time-dimension and one of the space dimensions (call it $x$). To make life easier, we choose our units of $x$ an $t$, such that the speed of light is equal to 1. (We can, for example, achieve this by measuring time in years and distance in light-years. Then the speed of light is $c = 1$ light-year/year). This means that light-rays travel on 45°-angles in our diagram.
The 45° line in the middle represents the event horizon. Every point left of that line is inside the black hole, every point to the right is outside. This construction makes it impossible for a light ray to leave the black hole, because it's angle relative to the $t$ axis would be more than 45°.
Now, let's draw the paths that you feet and your head take through space-time as you fall into the black hole. If your feet reflect a light-ray and you want to know at which point (in space AND in time) it reaches your head, you just have to draw a 45° line and see where it intersects with the trajectory of your head. Now, imagine your feet reflect a light ray at the exact point where they pass the event horizon. The light ray now travels along the event horizon and it arrives at your head at the exact point where it passes the horizon.
Thus, you will be able to see your feet at every point during the journey.
Lenard Kasselmann
- 1,374