Is coherent light required for interference in Young's double slit experiment?

Question

In this Veritasium video, a home experiment is presented which appears to produce a very good double-slit interference pattern with normal sunlight.

The experiment is an empty cardboard box with a visor and a placeholder for a microscope slide with two slits on one side. This is arranged with the slits and visor facing the Sun, so the interference forms on the bottom of the box.

They claim to observe a good interference pattern from the two slits:

Discussions of interference in optics textbooks often stress that coherent light is needed to produce such patterns, and that sunlight and other thermal sources of light do not have such coherence. How, then, is this possible?

Answer 1

Yes coherent light is required. The important thing to realize is that coherent light is not something that is magically created by lasers. Sunlight is somewhat coherent and it's easy to make it as coherent as you like.

What do people mean when they say "coherent light"? Well, it can be a few different things, but the relevant criteria in this context are:

• The light is all travelling more-or-less in the same direction ("spatial coherence" or "collimation")
• The light is more-or-less the same frequency ("temporal coherence" or "monochromaticity")

(See Footnote.)

I say "more or less" to emphasize the fact that it is never 100% coherent, (even from a laser), and it is never 0% coherent (even from a lightbulb or sunlight)

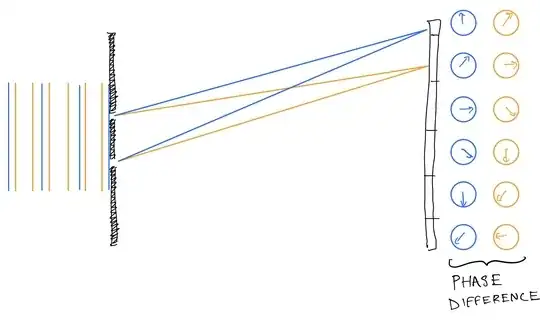
The way to think about it is, the light travelling towards the double-slits coming from a certain direction (e.g. 10 degrees away from normal incidence) create a really nice sharp double-slit pattern. The light travelling towards the double-slits from a different direction (e.g. 20 degrees away from normal incidence) also creates a really nice sharp double-slit pattern, but shifted!

So if you have light coming from every direction between 10 degrees and 20 degrees, you see a blurry composite of all those different double-slit patterns. It's possible that it will be so blurry that you can't even see that there's any pattern there -- it's just blurred out into a smooth line. But it's also possible that it will be only a little bit blurred out and the pattern is still recognizable.

The reason there's a cardboard box in the youtube video is to ensure that all the light from the sky that makes it to the slit is travelling in more-or-less the same direction. (Do you see how that could be done? Take a cardboard box, poke a small hole in it, and then put a double-slit far from the hole ... all the light at the double-slit is now coming in the same direction, i.e. from the hole.)

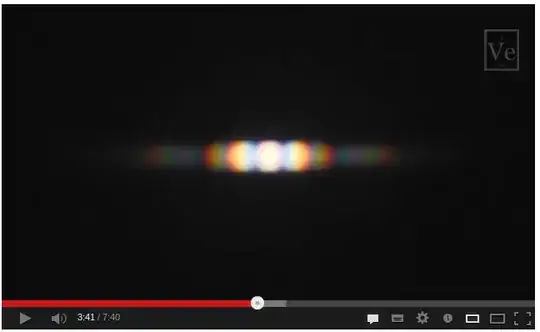
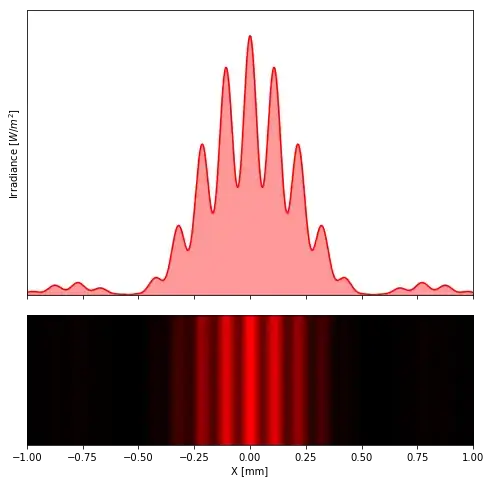
Frequency (or wavelength) is basically the same: Different frequencies of light make different interference patters, and we see a blurry composite of all those different patterns at once. If more monochromatic light was used (e.g. red laser light), the pattern would be much less blurry and easier to see, especially far from the center of the pattern. Luckily we have color vision, so we can (to some extent) recognize the composite pattern for what it is -- we see rainbows near the center, not just a blur.

--

Footnote: In comments, people are complaining that the term "coherent light" should refer only to spatial coherence, not temporal coherence. I disagree: The term can refer to either of these, depending on context. For example, in the context of optical coherence tomography, or in the context of "coherence length", or in the context of Michelson interferometers, people routinely use the phrase "coherent light" to mean temporal coherence.

Answer 2

“Interference is observed only when the light from the slits is coherent” (by the way, coherent light is defined as having all photons in the same phase, not just about the same wavelength and direction, as one answer here seems to suggest.) The statement can be challenged on three grounds:

1. Experiment. The Young's double slit experiment predates the laser. Light from a filament lamp produces a satisfactory interference pattern, provided it is approximately monochromatic, and provided that it is nearly parallel. It is a straightforward matter to replicate the experiment, without the need for a laser.
2. Theory. I quote the great physicist Paul Dirac (The Principles of Quantum Mechanics, Oxford Science Publications, Fourth Edition, p 9) “If the two components are now made to interfere, we should require a photon in one component to be able to interfere with one in the other. Sometimes these two photons would have to annihilate one another and sometimes they would have to produce four photons. This would contradict the conservation of energy. The new theory, which connects the wave function with the probabilities for one photon, gets over the difficulty by making each photon go partly into each of the two components. Each photon then interferes only with itself. Interference between two different photons never occurs.”
3. More experiment. This latter statement has been tested experimentally by performing the double slit experiment with photographic film and light of a very low intensity. The intensity is so small that the photons pass through the apparatus effectively one-at-a-time, with the average interval between two emitted photons much greater than the time required to pass through the apparatus, so that the probability of two photons “meeting” at the slits, although not zero, is very small. The interference pattern which builds up on the film is precisely the same as when high intensity light is used.

It has been argued that light from say a filament lamp is usually passed through a single narrow slit (as well as a colour filter) before arriving at the double slits. Without this “coherer”, the interference pattern is not observed. While experimentally true, the explanation is erroneous. Two incoherent photons arriving at this slit do not suddenly become coherent because they pass though a small hole together.

The whole thing is resolved as follows: A. Light for the double slit experiment must be nearly monochromatic so that the fringe separation is about the same for all photons, otherwise the interference patterns will form an indiscriminate jumble. B. Light for the double slit experiment must be nearly unidirectional (parallel) otherwise the interference patterns formed in all the slightly different directions behind the two slits will form an indiscriminate jumble.

These two conditions can be met by passing light from an incandescent lamp through a colour filter and a small hole, or by using a laser. The fact that laser light is also coherent is quite unimportant.

Answer 3

Here is Young's original experiment with light ( after having studied water waves)

The first screen generates a point source, so as to create a coherent wave . If it is a pin hole the geometry assures that all the photons come from the same original tiny source of light. Nice illustration here , page 5. Coherent means that the phases describing the mathematical form of the wave are not randomized.

In the video above the slits must be narrow enough and the distance between them small enough so that the wavefront arriving at them is similar to a point source wavefront.In any case the interference pattern is sort of blurred due to the many frequencies.

Answer 4

This question is answered with the Van-Cittert Zernike theorem. When the double slit experiment is performed with incoherent light the fringes get blurred. How much the fringes get blurred depend of how big is the light source and how far is the light source from the double slit.

The intensity pattern on the screen by the an incoherent source is given by:

$I ∝ sinc^2( \frac{ a}{z λ} x ) ( 1 + γ \cos(\frac{2D}{zλ} x))$

where:

$D$ = distance between the slits

$a$ = slits width

$γ$ is the degree of spatial coherence: $γ = sinc(\frac{2 D M}{L λ})$

$M$ = width of the light source

$z$ = distance from the screen to the double slit

$L$ = distance from the light source to the double slit

Interference fringes are fully visible when $γ = 1$ and they cannot be seen when $γ = 0$

When the experiment is performed with sunlight this formula gives for the coherence of the sunlight:

$L = 150.17$ million of km (distance from sun to earth)

$M = 1.3927$ million of km (diameter of the sun)

$D = 15 μm$

$λ = 500 nm$ (peak wavelength of the spectrum of the sunlight)

$γ = sin(\frac{2\pi DM}{Lλ}) ≈ 0.4$

So with this slits separation the light coming to the sun is partially coherent.

Plotting the pattern with the formula indicated above for z = 1m and a = 1 mm we get:

You can see in the plot that the fringes are still visible.

I made a video explaining and simulating how the double slit experiment with incoherent light works. Hope that it helps!

Answer 5

If the source is far away, light acquires a certain degree of coherence. Have a look at the Van Cittert–Zernike theorem, as pointed in wikipedia:

[...]the wavefront from an incoherent source will appear mostly coherent at large distances

The resulting fringes are different for different colors, but any color is maximum for straightforward direction. So, you see the bright spot at the center.

Then, the wavelengths our eyes are sensible to are not very different for this experiment. In other words, you may choose a distance between the slits such that wavelength/distance is the approx the same for all the frequencies your eye is sensible to (from red to blue), i.e. you choose a large distance. Then, the all frequencies between red and blue will approx peak at the same position. Blue will peak slightly before than red. From the figure, you indeed see the overlapping fringes given by the highest frequency you can see with your eyes (blue light) and the lowest (red light) soon afterwards.

Answer 6

This answer is in the domain of classical electrodynamics. For a quantum description, look at Bill Dixon’s answer.

Let us first see when an interference pattern occurs. On the screen, the intensity of light is given by the resultant field which is the sum of (to a great approximation) two fields. One from each slit. Assuming equal intensity of light from both the slits, the governing factor for the intensity at the screen is phase difference between the two fields.

To ensure a stable interference pattern all one needs to do is to ensure the phase difference between the fields of the two slits at the screen remain fixed. This is easy to ensure. If the field before passing through the slits is a plane wave, then the phase difference is fixed at all points on the screen.

To get plane waves (approximately) one uses a pinhole sufficiently far before the double slit that acts as a collimator. So finally you’ll see an overlap of $N$ double slit pattens for each of the $N$ different frequencies present.

Answer 7

The answer is no. Coherent light would be required for different photons to interfere with each other constructively, but as the quantum double slit experiment shows, individual photons effectively interfere with themselves, they do not need to interfere with other photons so coherent light is not required. Just as well since Young did not have coherent light.

But to get a good pattern of fringes requires monochromatic light, a filter, and all of the photons arriving at the twin slits coming from the same direction; an initial single slit achieves this. Young's experiment had the perfect set up.

Before reading this question I was unaware of the difference between spatial and temporal coherence, but it is not relevant here. Spatial coherence definitely does not just mean 'coming from the same direction'.

Answer 8

Newton and Young didn't have coherent light, they worked with white light and saw color fringes. But there is a second condition. The dimension of the light source has to be very small or the source has to be at a big distance (in relation to its dimension). In this cases the photons propagates parallel to each other and do not overlap each other on the observation screen.

Answer 9

This is possible because the pattern you see is made of coherent light. The source of the coherent light is the hole. Each color hits the screen where it is supposed to. If you only had one color you would notice the repeating pattern and it would be easier to realize that it was coherent. If you look close you will see where the colors repeat themselves over and over and over.

Answer 10

The following equations predict the phase difference between to light sources, when the light reaches a screen. These equations assume coherent light. In other words, the photons having the same phase when the photons leave the slit.

Constructive interference: d sin θ = mλ

Destructive interference: d sin θ = (m+1/2) λ For m = 0, 1, -1, 2, -2, … and d = distance between slits.

Compliance with these equations (a clean interference pattern) can indicate a high coherent light to random light ratio.