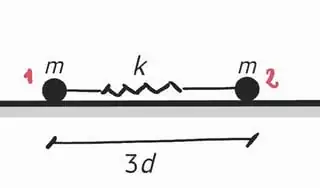
Two masses (indicated as 1 and 2) of value $m$ are connected by a spring with an elastic constant $k$ and a natural length $l_0 = 0$, as shown in the figure.
Initially, the two masses are separated by a distance of $3d$. From that position, they are released with no initial velocity. Since $l_0=0$, the spring compresses, bringing the two masses together.
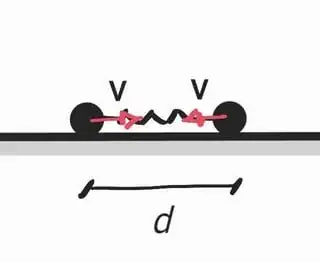
After some time, the two masses are at a distance $d$ from each other, and both have kinetic energy, as shown in the figure.
The principle of energy conservation states that $\Delta E = W_\mathrm{NCF}$, $\Delta K = W_\mathrm{all}$, and $\Delta U = - W_\mathrm{CF}$, where $E$ is the mechanical energy, $W_\mathrm{NCF}$ is the work done by non-conservative forces (both internal and external), $K$ is the kinetic energy, $W_\mathrm{NCF}$ is the work done by all forces (both internal and external), $U$ is the potential energy, and $W_\mathrm{CF}$ is the work done by conservative forces (again, both internal and external).
The only non-conservative force acting on this system is the normal force exerted by the floor. However, this force does no work because it is perpendicular to the direction of motion, and thus the mechanical energy must be conserved: $\Delta E = 0$.
This is not the case for the kinetic and potential energies, as one is transformed into the other. Therefore, we have $\Delta K > 0$, and there must be work done by conservative forces because, as I previously said, the normal force does no work.
The Question
The question is simple:
(Q1) Which forces do work to give the masses kinetic energy?
I have reviewed answers to other questions, but the matter is still not entirely clear to me. In particular, I found comments and ideas in the following posts:
- Isn't the work done on a spring-mass system zero, so that there is be no change in potential energy?
- Can internal forces do work?
- On work done by internal forces which is coming out to be not equal to zero
- Why is the spring force equal to the external force?
What I've Thought So Far
(1) Considering the System $\left( 1, 2 \right)$
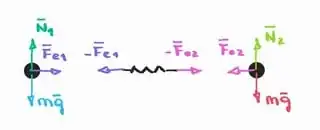
Things are clear in this case. The forces acting on the masses are their weights (which do no work), the normal forces exerted by the floor (which do no work), and the elastic force of the spring, as shown in the picture. All these forces are external (there are no internal forces) and both the weight and the elastic force are conservative.
In this case, the forces that do work are clearly the elastic forces that bring the masses towards the center of the spring.
(2) Considering the System $\left( 1, 2, \mathrm{spring} \right)$
If the spring is considered to be part of the system, then the elastic forces are internal and play no role in the conservation of linear and angular momentum. They do, however, play a role in the conservation of energy.
The problem is that if the spring is considered as part of the system, there are four internal elastic forces. The first one is the force that the spring applies to mass 1 $\mathbf{F}_{\mathrm{e}1}$, the second one is its reaction $-\mathbf{F}_{\mathrm{e}1}$ (the force that mass 1 applies to the spring), the third one is the force that the spring applies to mass 2 $\mathbf{F}_{\mathrm{e}2}$, and the fourth one is its reaction $-\mathbf{F}_{\mathrm{e}2}$. All of this is shown in the following picture.
Now, the total work done by the internal elastic forces is zero because there are equal and opposite forces on each side of the spring. Since they move in the same direction, their work cancels out.
This, however, cannot be correct because there is a change in kinetic energy, so work must be done (either by internal or external forces).
(Q2) In this picture, should the reaction forces acting on the spring be considered as part of the system? If not, this case is basically the same as the case for the other system but with the elastic forces as internal forces.
(Q3) If the elastic forces acting on the spring should not be considered, why would that be?