The following image taken from one of the books:
As it says, it moves to the dotted line which means box will move to the $x$ as well as $y$ direction.
In the same book, there's a vector product example as below, but I don't understand what $0$ means. I understand math, but not physics. Does 0 mean box won't move at all(but this contradicts the first picture). What does 0 mean?
What $\vec A \cdot \vec B = 0$ means is that the two forces are neither opposing nor assisting each other.
Note that it's a scalar value, with units of square-newtons, and is not something you'll see much in physics.
That it's a scalar means it has no information about direction of motion.
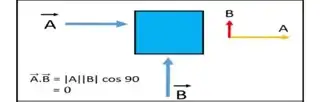
When the dot produt of two vectors is $0$, they are perpendicular to each other. The fomula in the picture is a special case of
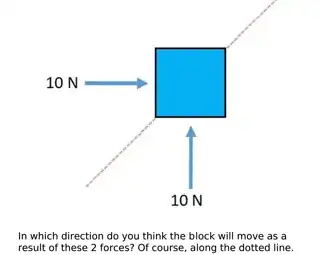
\begin{equation} \vec{A} \cdot \vec{B} = |A||B| \cos \theta, \end{equation} where $\theta$ is the angle formed by the vectors. If this angle is $90^\circ$, like in the picture, the dot product is $0$, and the forces act on perpendicular directions. Therefore the box will move, and the total motion will be that caused by force $\vec{A}$ added to that caused by force $\vec{B}$. Since the forces have equal magnitudes, you get that the box will move along the dotted line.
A way to see this clearly is to add the forces before finding the motion of the box. Since $\vec{A} = (10 N) \vec{x}$ and $\vec{B} = (10 N) \vec{y}$, where $\vec{x}$ and $\vec{y}$ are unit vectors pointing on the $x$ and $y$ directions, respectively, the total force will be \begin{equation} \vec{F} = \vec{A} + \vec{B} = (10 N) \vec{x} + (10 N) \vec{y} = (10 N) (\vec{x} + \vec{y}). \end{equation} The vector $\vec{x} + \vec{y}$ points along the dotted line in the picture, the diagonal, so that is the direction along which $\vec{F}$ pushes the box.
If this is not clear, you can convince yourself by taking the dot product of $\vec{x} + \vec{y}$ it with $\vec{x}$ and $\vec{y}$ and use the formula in the top, to find exactly what angle it makes with these two vectors. You should find that in both cases the angle is $1/\sqrt{2}$ radians, or $45^\circ$.
