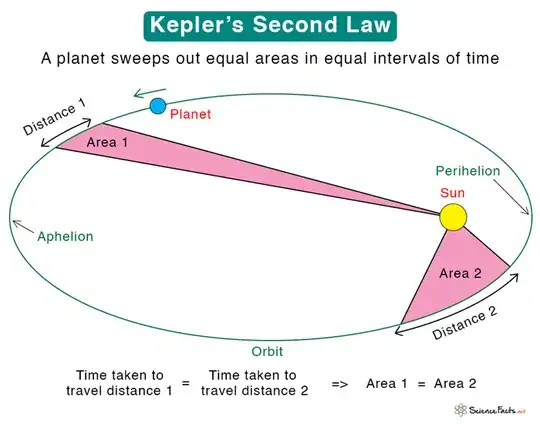
This is probably a very stupid question. We are told that due to Kepler's Second Law, which according to this very straightforward explanation:
"Kepler's second law of planetary motion describes the speed of a planet traveling in an elliptical orbit around the Sun. It states that a line between the Sun and the planet sweeps equal areas in equal times. Thus, the speed of the planet increases as it nears the Sun and decreases as it recedes from the Sun."
But it seems to me that a line between the Sun and the planet would always sweep out equal areas, regardless of its distance from the sun or how fast the planet is moving. What am I missing?