3

What characteristic of photons causes them to travel with constant speed in all frames of reference? Till the topics I have studied, we always assume this but never got any ideas what can be in the nature of photons (the quanta of electromagnetic field) that causes this. Maybe something is not clear to me. Please explain.

Qmechanic
  • 220,844
cleanplay
  • 1,555

3 Answers3

4

The reason can be found in the masslessness of photons. What this means is that the rest mass of the photon vanishes. This can be seen by analyzing the framework of special relativity, which is based on the observation that light is moving at the same velocity in all frames of reference.

The relativistic energy-momentum relation of a general particle is given by

$$E =\sqrt{(pc)^2+(m_0c^2)^2}, $$

where $p$ is three-dimensional momentum, $m_0$ is rest mass and $c$ is the speed of light.

So how can we see that for a particle moving at the speed of light, $m_0$ has to be zero?

A particle moving through Minkowski space can be classified in terms of its momentum vector. It can be either timelike (velocity smaller than c), lightlike (also called "null", velocity equal to c) or spacelike (velocity larger than c). For reference, see the diagram below (source: Wikipedia).

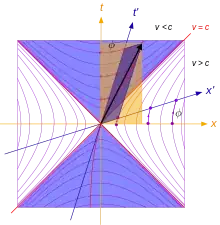
enter image description here

The condition for a vector to be lightlike is that the square of its norm has to vanish. The momentum-four vector in special relativity is given by

$$\textbf{P}=(\frac{E}{c},p_x,p_y,p_z)$$,

with

$$\textbf{P}^2=-\frac{E^2}{c^2}+p^2, $$

where $p$ is the norm of the spatial components, where I have assumed the Minkowski signature to be $(-,+,+,+)$. If this expression is equal to zero, we arrive at the relation

$$-E^2/c^2+p^2=0,$$

or

$$E=pc.$$

When we compare this to the relativistic energy-momentum relation I have written down above, we see that the two expressions are consistent if the ress mass $m_0$ vanishes. This should give some insight on how the two concepts of masslessness and moving at the speed of light in all reference frames are related.

Frederic Brünner
  • 15,932
1

They travel at the speed of light because they have zero mass.

Enucatl
  • 639
-1

I am postulating that they may be driven forward or repelled by the fabric of space and not by the initial velocity imparted to them when they are created i cant back it up with any data as yet but it may explain why they don't slow down over long distances and encountering masses

terry1234
  • 1