How does a lever arm increase force?

Question

A lever and a fulcrum is able to to multiply the input force to the output force and trade moving distance for increased force. The same happens in automobile transmissions, taking advantage of high motor RPMs.

What exactly is the physical mechanism behind this? I am very aware you can mathematically prove it, for instance via an energy approach where energy in roughly equals energy out. Still, is it possible to explain the phenomena down to atomic level? That is, how is it in qualitative terms, that the force on the other side of the lever is amplified?

Answer 1

The "extra" force is generated by the fulcrum. Consider the following setup:

We load a seesaw with a weight of 1 and 3. The fulcrum has to supply a force of 4 in the opposite direction, otherwise the net force is not zero and the seesaw would accelerate through the fulcrum. In the setup above, the seesaw is perfectly balanced. We know this because the net torque around the fulcrum is zero: $\tau=\sum_ir_i\times F_i$. It's as if the lever multiplies the force, but the force is supplied by the fulcrum. Due to the fact that torque scales with distance, we have that in equilibrium the largest force is the closest to the point of rotation.

You may still not be convinced, because the seesaw is not doing useful work. Consider the same bar of 4 units long, but now we want to pry open a crate using our lever. At one end we are pushing down and the other two ends are stuck. Consider the scenario where you are pushing down, but the crate/lever is not moving yet. Once again, the total force and total torque must be zero. So the force in the middle must be larger than the rightmost force to ensure a net force of zero. You can add an arbitrarily large force couple to the forces that touch the crate and still have a net force of zero, so this leaves one degree of freedom. We can use the fact that the torque must be zero again to show that the center/right forces are larger than the input force.

So why can you create large forces with a lever? I would say two things:

1. When two objects are pressed together, they create a normal force at the surface. This normal force can arbitrarily large, provided the objects don't break.
2. Torque scales with lever arm.

Answer 2

You can think through the mechanics of this phenomenon with a bendy lever.

Suppose you press down at one end that is 3 m from the pivot and the other end is 1 m from the pivot in the other direction. The first thing that happens is that the point you press goes down, which pulls the part next to it down too. By how much? Let's view the lever as having 4 equal parts, 3 on your side. Your pressing causes the 1st part to bend, which causes the 2nd part to bend, and so the 3rd part bends too, and of course finally the 4th part. If the lever's pivot and opposite end is fixed, this will reach an equilibrium in which they all bend the same amount, since any part that is more bent will cause its neighbours to bend more instead.

Here is a highly exaggerated diagram of the bendable lever in an equilibrium state:

Now every part is the same, and each bends by an amount roughly proportional to the bending stress on it, which is just how strongly one end is twisted relative to the other. At equilibrium, the bending stress is identical in every part. Thus the end of the lever that you press down moves 3 times as much as the other end of the lever. The force exerted at a point by a part is proportional to the difficulty in moving that point, so the end of the lever that you press down is 3 times easier to move than the other end.

Therefore the force you exert on your end is 1/3 of the force that the other end exerts.

Note that you can also figure out the force at the pivot relative to your end by exactly the same reasoning, simply treating the other end as the immovable pivot instead, and so the force you exert on your end is 1/4 of the force exerted at the pivot.

Answer 3

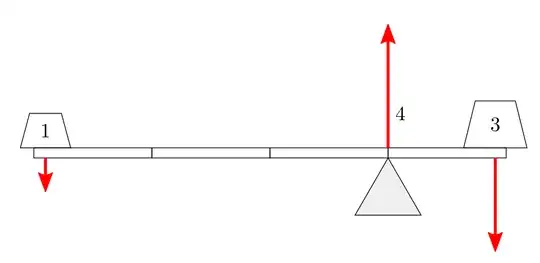
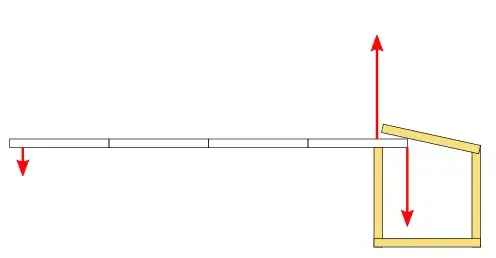
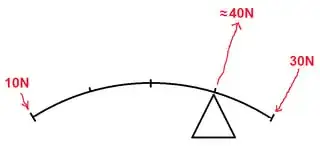
You can look at this from the perspective of energy conservation.

The force applied to the long side of the lever is doing work, and because of energy conservation the short side of the lever is doing the same amount of work on its load.

$$W_{\text{in}} = F_{\text{in}} \cdot X = W_{\text{out}} = F_{\text{out}} \cdot Y$$

The distance that the long and short sides can move is constrained by the mechanics of the system. Therefore, the output force is the only variable that can account for the necessity of energy conservation.

In other words, X > Y requires that F(out) > F(in). As we know, the force multiplier is proportional to the ratio of the lengths of the levers.

$$F_{\text{out}} = \frac{X}{Y} \cdot F_{\text{in}}$$

Essentially, energy conserved everywhere in the system. At the contact points on the lever, and everywhere in the lever. Applying force to one side of the lever transmits force through the atomic bonds in the lever, and out the other side. From the classical perspective, it's Newton's Third Law in action.

As a counter example, if the lever was elastic, then the lever could flex and the simple proof above would not be true. Energy would be absorbed by the lever and the fulcrum and converted to heat or deformation.

So, it's the integrity of the rigid lever that requires this to be true, otherwise the lever would not be a rigid lever at all.