Why don't we put satellites into an orbit where there is (almost) no time dilation/contraction compared to Earth's surface?

Question

Consider:

On this image, if I understand correctly, the time dilation diagram is shown depending on the height for circular orbits. First in low orbit, time slows down relative to the surface due to high speed, but for higher orbits, speed and gravitational dilation is lowering, so at roughly 3,200 km elevation, time passes almost at same rate as on the surface!

However, GPS satellites are mostly located at about 20,000 km. In that case, why don't we place GPS satellites at an altitude where time passes at the same rate as on the surface? (Of course, in this case, too, corrections would have to be made for different speeds of the Earth's surface at different latitudes, but perhaps at an altitude of 3,200 km, this would be much easier to do?)

Answer 1

The higher the satellite's orbit, the more of the Earth it can see (and hence the fewer satellites you need to ensure complete coverage of the Earth). The particular orbits chosen for navigation satellites also have the advantage that they take an integral fraction of a day to complete, so the ground track of the satellites is easier to predict.

Furthermore, in a low or medium earth orbit, there is still a non-trivial amount of atmospheric drag. So these satellites would require significant amounts of propellant or frequent refueling to ensure that their orbits don't decay. Given the expected lifespan of GPS satellites, this would be extremely expensive. This further complicates matters by making the location of the satellite less predictable.

The cost of adjusting for time dilation is really trivial (it's a simple matter of scaling the clock), whereas the costs of using the lower orbit where time dilation is not a factor would be very high -- the ground track would be harder to calculate, and more satellites would be required. The cost of adding even a single satellite would be vastly, vastly higher than the cost of putting a simple scaling circuit (or software) into all of the satellites.

Answer 2

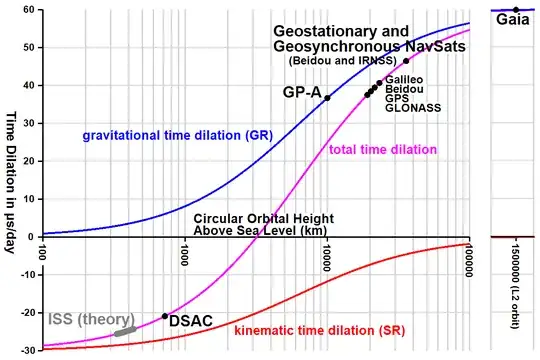
You have to differentiate between corrections that are sources of error and corrections that are well understood and can be accounted for.

Time dilation is a well understood effect, and if you wanted to do something like sync two clocks on earth by having a satellite simultaneously send signals to both clocks (a pretty common timing-metrology technique), you definitely need to account for the time dilation between the two earth clocks and the satellite. And you can do that by tracking the satellite's position and using the relevant equations to find the expected time dilation effect. We aren't in the business of spending several million to put a satellite into orbit, but putting it at 3200km because "ehh... I don't want to write the code to account for time dilation."

However this can become a source of error if there is any uncertainty on the position of the satellite. In which case, actually, you'd want your satellite to sit in a place where the slope of this curve is smallest - not where the total effect is smallest. Since the horizontal axis is logarithmic, it's always better to be higher.

To prove this, say we had a measurement of the satellite's height $h_0$, and some error on that height $\delta_h$. And let's say the time dilation at a height $h$ is $T(h)$. Then the error on the time dilation effect is $T'(h_0)\delta_h$.

All that being said - I do agree it's interesting, and surprising to me, that there's a height at which circularly orbiting satellites have zero time dilation relative to Earth's surface.

Answer 3

It's probably worth adding that the altitude you're talking about is in the inner Van Allen radiation belt, which extends from about 1,000 to 12,000 km above the surface. Any satellites at that altitude would need additional radiation shielding for their electronics.