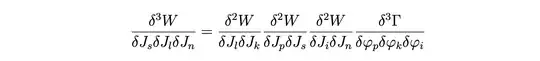3

This is a follow-up question to my earlier post. The Schwinger–Dyson equation on Peskin and Schroeder reads (p.308): $$ \left\langle\left(\frac{\delta}{\delta\phi(x)}\int d^4x'\mathcal L\right)\phi(x_1)...\phi(x_n)\right\rangle = \sum_{i=1}^n \left\langle\phi(x_1)...(i\delta(x-x_i))...\phi(x_n)\right\rangle \tag{9.88} $$

This equation tells us that the classical Euler-Lagrange equations of the field $\phi$ are obeyed for all Green’s functions of $\phi$, up to contact terms arising from the nontrivial commutation relations of field operators.

I also found this reference pretty helpful to study this equation. Starting from equation (5):

$$ \frac{\delta\Gamma}{\delta\phi_i} = -J_i\tag{5} $$

We can differentiate this equation twice to obtain a relation which connects the three-point connected Green function with three-point vertex part (eq. (7)):

enter image description here

Where $W[J]$ is the generator of all connected Green’s functions. We may continue and once more differentiate to obtain the relation between four- and three- and two-point Green functions, as shown in eqn. (9) in the paper, and this is called the Schwinger-Dyson equation.

I am confused about how the Schwinger-Dyson equation is represented. Does Peskin and Schroder's form the same as the one that presented in this paper?

Qmechanic
  • 220,844
IGY
  • 1,853

2 Answers2

1

For example, let’s consider the following Schwinger-Dyson equation. $$0=\int D\phi\frac{\delta}{\delta\phi_y}\Big(e^{iS(\phi)+i\int_xJ\phi}\Big)$$ Taking the derivative about $\phi$, we may obtain \begin{align}0&=\int D\phi\Big(\frac{\delta S(\phi)}{\delta\phi_y}+\int_xJ_x\delta_{x,y} \Big) e^{iS(\phi)+i\int_xJ\phi}\\ &= \int D\phi\Big(\frac{\delta S}{\delta\phi_y}\Big(\frac{\delta}{i\delta J}\Big)+\int_xJ_x\delta_{x,y} \Big) e^{iS(\phi)+i\int_xJ\phi}\\ &=\Big\{-(\Box+m^2) \frac{\delta W}{\delta J}+J\Big\}Z\\ \therefore &\ \ (\Box+m^2) \frac{\delta W}{\delta J}=J\\ \therefore &\ \ (\Box+m^2) \frac{\delta W}{\delta J_x\delta J_y}=\delta_{x,y} \end{align} This is the Schwinger-Dyson equation for the connected Green functions. The Klein-Gordon operator on the left-hand side is extended to $\frac{\delta\Gamma}{\delta\phi\delta\phi}$ in quantum terms. In this sense, the relational expression between the connected Green functions and the vertex functions is sometimes called the Schwinger-Dyson equation. More general equation can be obtained by taking the derivative about J.

Siam
  • 1,620
1

  1. Eqs. (5) and (7)-(9) in Ref. 1 are just consequences of the Legendre transformation between the generating functional $W_c[J]$ of connected diagrams and the effective/proper action $\Gamma[\phi_{\rm cl}]$, cf. e.g. this Phys.SE post.

  2. A standard consequence of the Schwinger-Dyson (SD) equations is $$\left<\frac{\delta S[\phi]}{\delta \phi^k}\right>_{\!J}~=~-J_k.\tag{A}$$

    In contrast Ref. 1 effectively considers the following main identity$^1$ $$\begin{align} \exp&\left\{\frac{i}{\hbar}W_c\left[J\!+\!\frac{\hbar}{i}\frac{\delta}{\delta \phi_{\rm cl}}\right]\right\}\left.\frac{\delta S[\phi_{\rm cl}]}{\delta \phi_{\rm cl}^k} \right|_{\phi_{\rm cl}=0}\cr ~=~&Z\left[J\!+\!\frac{\hbar}{i}\frac{\delta}{\delta \phi_{\rm cl}}\right]\left.\frac{\delta S[\phi_{\rm cl}]}{\delta \phi_{\rm cl}^k} \right|_{\phi_{\rm cl}=0}\cr ~=~&\int\! {\cal D}\frac{\phi}{\sqrt{\hbar}} \exp\left\{\frac{i}{\hbar}(S[\phi] +J_{\ell}\phi^{\ell})+\phi^{\ell}\frac{\delta}{\delta \phi^{\ell}_{\rm cl}}\right\}\left.\frac{\delta S[\phi_{\rm cl}]}{\delta \phi_{\rm cl}^k} \right|_{\phi_{\rm cl}=0}\cr ~=~&\int\! {\cal D}\frac{\phi}{\sqrt{\hbar}} \exp\left\{\frac{i}{\hbar}(S[\phi] +J_{\ell}\phi^{\ell})\right\}\frac{\delta S[\phi]}{\delta \phi^k}\cr ~\stackrel{(A)}{=}~&-J_kZ[J], \end{align}\tag{B} $$ compare with e.g. eq. (10) for $\phi^4$ theory and eqs. (12)-(14) for QED.

References:

  1. B.A. Fayzullaev & E. Qayumov, SD type equations for some QFT models, arXiv:2006.04908.

--

$^1$ Eqs. (3) and (6) seem different from eq. (B) as $\phi_{\rm cl}$ is presumably not put to zero.

Qmechanic
  • 220,844