The notion that a spacetime can be decomposed into a spacelike and timelike part is generally called a spacelike foliation, where your spacetime manifold can be decomposed into purely spatial submanifolds at a given point in time :
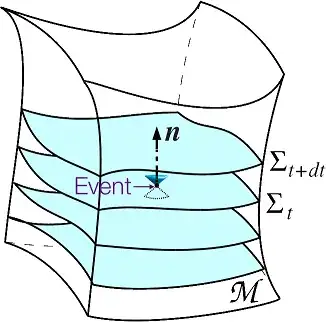
Spacetime in general relativity is always locally like Minkowski space, as the saying goes. In some sense, it is always possible to generate some local coordinates in which you can split the spacetime into a spatial and timelike part like that.
There are many ways to do this, but consider this example : at a given point $p$, the tangent space $T_p M$ just looks like Minkowski space. You can assign some orthonormal basis $\{ e_\mu\}$ there, where $e_0$ is a timelike vector and the remaining vectors are spacelike.
Around this point $p$, there exists a neighbourhood $U_p$ which maps a subset of the tangent space $T_p M$ to $U_p$ bijectively : every vector corresponds to a point in that neighbourhood and vice versa. The map is the exponential map at $p$, $\exp_p : T_p M \to U_p$, and it is usually constructed for instance by considering geodesics (with proper time parametrization) emanating from $p$ with a tangent vector $v$.
This defines a set of coordinates on the manifold which are very close to Minkowski space, and certainly allow for a decomposition into time and space. The time coordinates are simply the flow of the $e_0$ vector, appropriately parallely transported around, and the same goes for the spatial coordinates. Furthermore, if you define a foliation of $T_p M$ into spacelike slices (as you can generally do), this corresponds to a foliation of this neighbourhood into such slices as well.
The problem of general relativity here is that this neighbourhood generally has a finite extent. The exponential map fails to be bijective at some point (the cut locus), meaning that two curves starting at $p$ with different directions end up at the same point, therefore no longer making valid coordinates at that point (physically this would correspond for instance to two objects shot in different directions eventually crossing paths, for instance as in the case of gravitational lensing). This isn't necessarily to say that you can no longer split spacetime into time and space beyond that point, but the most basic method to do so will no longer work.
The range in which we can use this is called the injectivity radius of the exponential map. It's a pretty hard quantity to estimate, but as far as I know it isn't an issue for any body inside the solar system for instance (although you can get Einstein rings for the observation of other stars), to give you an idea of the scales involved.
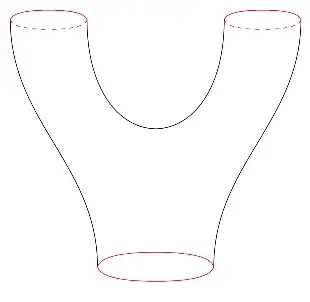
If you can't extend such coordinates like that, it is still possible (and in fact quite likely) that spacetime can still be decomposed in such a way. You can find counter examples. For instance the pair of pants spacetime (where some initial region splits into two after some time) admits no such global decomposition into a time and space part :
The Gödel spacetime also admits no such foliation. There is no way to say, even conventionally, if two events occurs simultaneously in there.
The root of those issues is quite complex. On a formal level this is due to the lack of an integrable distribution on those spacetimes : there's no set of 3 spacelike vector fields on that spacetime that can be both the tangents of a 3-submanifold foliation and also complementary to a foliation by timelike vectors.
While this issue isn't entirely down to causality issue (plenty of non-causal spacetimes admit such a foliation), it is true that if a spacetime's causality is well-behaved enough, it will admit such a foliation. If a spacetime is stably causal, there exists a foliation into spacelike hypersurfaces. This roughly means that 1) there's no closed timelike or causal curves (objects can't intersect themselves in the past) 2) those curves can't also be almost closed 3) you can't have such problems even if you change the metric a little bit.
As those are very mild conditions on causality, it is usually assumed that spacetimes can indeed be decomposed like that. If you strengthen those causal conditions a little bit into being globally hyperbolic, you have furthermore the condition that all the spatial slices are identical, and your spacetime has the topology $\mathbb{R} \times \Sigma$, with the line $\mathbb{R}$ being time and $\Sigma$ being some spatial manifold.
Beware that such decompositions aren't unique. Much like in special relativity, where the equivalent is the consideration of simultaneity surfaces, we can choose a wild variety of such decompositions. If the spacetime can be decomposed but is still fairly ill-behaved, it's even possible that different foliations will have wildly different properties, such as having different topologies for the spatial slices.
But overall, those are very theoretical considerations. As far as we can tell from observations, our spacetime is very boring in that respect, and can be decomposed into time and space without too much worries, as long as you keep in mind that those are choices that one has to keep track of. If you are worried about actual astronomical observations for instance, you can check some of the "official" astronomical spacetime coordinates[1][2] used in the field, which are very much considering a split into time and space.

