What is the physical meaning of the imaginary part in $LRC$ circuits or AC circuits?

Question

When we learned about AC L-R-C circuits, there is a phase difference in the voltage across the inductor and capacitor with the current. We were told that representing these phase differences on the complex plane and extracting the real part can make calculations less complicated. However, I see that the impedance of the capacitor and inductor both has an imaginary number $i$ in it, i.e. $1/(iwC)$ and $Lwi$. So does the complex part actually has a physical meaning? How does this i relate to the $e^{iΘ}$, where I know $e^{iwt}$ represents $coswt$, which represents an oscillatory relationship?

Answer 1

. . . . . can make calculations less complicated.
This is indeed the case.

In ac circuits the voltage and current are not necessarily in phase and the introduction of complex numbers and the use of the complex plane makes a lots of the analysis much simpler.

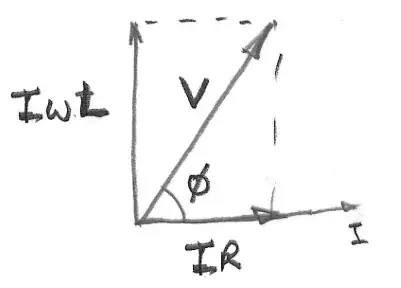
Suppose that the ac current if $I\cos(\omega t)$ then if there is as series LR circuit the voltage across the resistor is in phase with the current, ie of the form $V_{\rm R} = IR \cos(\omega t)$, and the voltage across the inductor is $\pi/2$ ahead of the current, ie of the form $V_{\rm L} = I\omega L \cos(\omega t+\pi/2)$.

To find the voltage across the two components one must add these voltages, evaluate $IR \cos(\omega t) + I\omega L \cos(\omega t+\pi/2)$.
This can be done using trigonometrical relationships but the use of complex numbers remove that chore.

Taking the voltage across the resistor as the real part of $IRe^{i\omega t}$ and the voltage acros the inductor as the real part of $\omega Le^{i\omega t+\pi/2}=(\omega L e^{i\pi/2})e^{i\omega t} =i\omega L e^{i\omega t}$.

After adding, $(IR + iI\omega L)e^{i\omega t}= \sqrt{(I^2R^2+\omega ^2L^2)}e^{i\tan^{-1}(\omega L/R)}e^{i\omega t} = \sqrt{(I^2R^2+\omega ^2L^2)}e^{i(\omega t+\tan^{-1}(\omega L/R))}$

Now looking at the real part of this expression gives the sum of the two voltages as $\sqrt{(I^2R^2+\omega ^2L^2)}\cos(\omega t+\tan^{-1}(\omega L/R))$as shown by a diagram drawn in the complex plane.

With V = $\sqrt{(I^2R^2+\omega ^2L^2)}$ being the magnitude of the voltage across the two components and that voltage leading the current by $\phi = \tan^{-1}(\omega L/R)$.