2

I have already calculated the divergence of the electric field, i.e.

$$\vec{\nabla} \cdot \vec{E}(\vec{r})=\left( \begin{array}{rrr} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \\ \end{array}\right)\cdot \frac{Q}{4 \pi \epsilon_0}\left( \begin{array}{rrr} \frac{x}{(x^2+y^2+z^2)^{\frac{3}{2}}} \\ \frac{y}{(x^2+y^2+z^2)^{\frac{3}{2}}} \\ \frac{z}{(x^2+y^2+z^2)^{\frac{3}{2}}} \\ \end{array}\right)=0$$

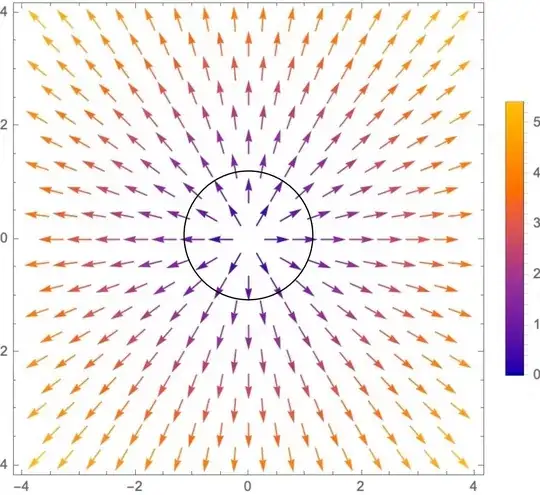
Unfortunately, I am now having trouble interpreting the result physically. If we assume that we are dealing with a positive point charge which is located at the origin of the coordinate system, then the electric field lines of this positive point charge for the 2D case would look like this.

enter image description here

Unfortunately, I do not yet know how to plot electric field lines in mathematics, so I have represented the field lines as vectors.

I always explain the divergence with the help of the flux through a surface. I have now drawn a circle as the surface. The normal vectors are parallel to the field lines of the charge, so I get a positive flux, which means that the divergence must be positive, and it must be a source in the center of the circle.

I understand why with the magnetic field the divergence and thus the flux are zero, because every field line that penetrates the surface reenters the surface at another point, which is why the flux is zero and thus also the divergence

But why is the divergence for a point charge also zero?

Qmechanic
  • 220,844
Lambda
  • 85

1 Answers1

3

You need to be careful where you apply your formula, because it is ill-defined at the origin. Actually the divergence is zero everwhere outside the origin (because there is no charge). And it is infinite at the origin (where the point charge is).

$$\begin{align} \vec{\nabla} \cdot \vec{E}(\vec{r})=\begin{cases} 0 & \text{, if } \vec{r}\ne\vec{0} \\ \infty & \text{, if } \vec{r}=\vec{0} \end{cases} \end{align}$$

If you are familiar with the Dirac $\delta$-function, you can summarize the above to $$ \vec{\nabla} \cdot \vec{E}(\vec{r})=\frac{Q}{\epsilon_0}\delta^3(\vec{r}).$$ Writing it this way also includes the fact $\int\vec{\nabla}\cdot\vec{E}(\vec{r})d^3r=\frac{Q}{\epsilon_0}$, which follows from the defining feature of the Dirac $\delta$-function: $\int\delta^3(\vec{r})d^3r=1$.

Thomas Fritsch
  • 42,352