0

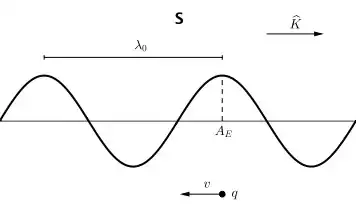
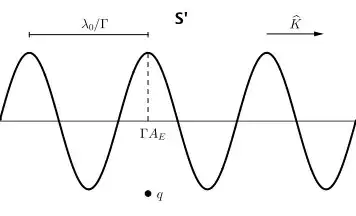
Special Relativity can be used to show that the magnetic force on a charge in parallel motion next to an infinite wire can be understood as an electrostatic force (when viewed from the rest frame of the charge). There are several posts and nice YouTube videos that explains this.

But how does this work in the case of light waves? Here magnetism cannot be an electrostatic effect in the rest frame, since no charges are present to produce the static field. So, from the perspective of special relativity, what causes the magnetic force of light in the rest frame of the charge?

(As a sidenote, I am also aware that the magnetic force is not an electrostatic effect in general. For non-parallel motion dynamic equations must be used, as this textbook shows)

Qmechanic
  • 220,844
Mads Vestergaard Schmidt
  • 314

1 Answers1

-2

In short, what is experienced as a magnetic force in the moving frame of the charge, is experienced as an electric force in the rest frame, due to the Doppler shift of the amplitude of the electric wave. Einstein published the following amplitude transformation equation in 1905.

\begin{equation} A’ = \gamma\left( 1 - \beta \cos \theta \right) A \end{equation}

If we evaluate the combined electric and magnetic force in the moving frame, and the purely electric force in the rest frame, we can link them with the relativistic force transformations. When we do this, the amplitude transformation above can be derived. This shows us that the magnetic force of the wave accounts for the change in electric force the moving charge experiences, due to the Doppler amplitude shift of the electric wave it interacts with, in the rest frame perspective. You can find the derivation and full explanation in this preprint.

S

Electric wave with amplitude $A_E$ and wavelength $\lambda_0$ in the moving frame. The charge $q$ moves to the left with $v$ while the wave propagates to the right along $\hat{K}$.

S'

Same situation viewed in the rest frame of the charge. The Amplitude is now altered by the factor $\Gamma=\gamma\left( 1 - \beta \cos \theta \right) A_E$, and the wavelength by the factor $ \frac{1}{\Gamma} $.

Mads Vestergaard Schmidt
  • 314