How can an irreversible isothermal process exist?

Question

An isothermal process is one in which temperature of the gas is constant throughout the process.

From my physics textbook:

the state of a gas is described by specifying its pressure $p$, volume $V$ and temperature $T$. if these parameters can be uniquely specified at a time, we say that the gas is in thermodynamic equilibrium.

This is always the case in a reversible process, but if we cannot specify temperature during an irreversible process, how can we say that during an irreversible isothermal process, the temperature of gas remains constant throughout?

Answer 1

how can we say that during an irreversible isothermal process, the temperature of gas remains constant throughout?

As @Chet Miller pointed out in his answer, the term "isothermal", or constant temperature, in connection with an irreversible process refers only to the temperature at the boundary between the system and surroundings, where the surroundings is considered to be an ideal (constant temperature) thermal reservoir. Since there can only be one temperature at a specific location, and given that the temperature of an ideal thermal reservoir at the boundary is considered constant (which in reality is isn't), then so must the temperature of the gas at the boundary be considered constant.

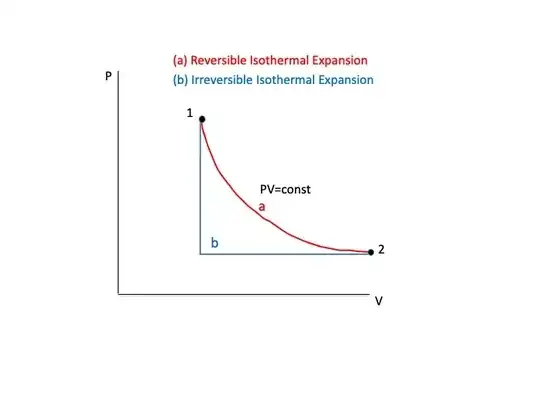
As a practical matter, for want of a better term, one uses the term isothermal for an irreversible process carried out in a constant temperature surroundings to distinguish it from a reversible process carried out in the same constant temperature surroundings. See the figure below.

For the reversible isothermal expansion the external pressure is gradually reduced so that both the pressure and temperature throughout the gas, not just at the boundary with the surroundings, is always in equilibrium with the surroundings.

For the irreversible process the external pressure is suddenly reduced (e.g., suddenly removing a weight from atop a piston) and the gas allowed to expand rapidly (irreversibly) until pressure and temperature equilibrium is reestablished. During the irreversible expansion the temperature and pressure of the gas is only the same as the surroundings at the boundary (pressure because of Newton's 3rd law). Beyond the boundary, however, temperature and pressure gradients exist.

Hope this helps.

Answer 2

(a) the state of a gas is described by specifying its pressure , volume and temperature .

This is not an incorrect statement, but is a little puzzling, because for a gas we need only to specify any 2 of these variables; the third is then known from the equation if state. For example, for an ideal gas the equation of state is $pV=nRT$.

(b) Here is an example of an irreversible isothermal process for a gas... A fan, driven by an electric motor, is set rotating in a leak-proof cylinder of gas. The gas temperature rises, but more and more slowly, because heat escapes at an increasing rate to the surroundings through the walls of the cylinder. Eventually the gas reaches an equilibrium temperature (with negligible variation over the volume of the gas), when work done on the gas by the fan is transferred to heat at a constant rate, and we have an irreversible isothermal process.

Note: I'm using heat in the thermodynamic sense of energy (entering or) leaving as system because of a temperature difference between the system and its surroundings.

If we're not restricted to gases, a very simple example of an irreversible isothermal process is water boiling in an electric kettle. Electrical work is transferred irreversibly to heat and to intermolecular energy in the steam, at a constant temperature of approximately 100°C.

Answer 3

To complete the previous answers, we can also cite the example of a chemical reaction. If the kinetic reaction rate is slow enough to allow thermalization processes, the reaction can be carried out isothermally and at constant pressure while being evidently irreversible.

Answer 4

Some people, myself included, consider an irreversible isothermal deformation of an ideal gas as one in which the boundary temperature at the interface between the gas and its surroundings is held constant at the initial gas temperature (i.e., gas in contact with ideal constant temperature reservoir) throughout the process until thermodynamic equilibrium is re-achieved. Of course, in such a process, internal temperatures within the gas are not spatially uniform.

Answer 5

It is the uniformity of pressure and temperature throughout the system that defines the equilibrium state. To avoid the ambiguity of the meaning of $p$ and $T$ in non-equilibrium states, consider a non-equilibrium partitioning of the system: a rigid insulated is box divided into two parts, each part is in internal equilibrium with its own pressure and its own temperature. The partitioning represents a non-equilibrium state for the entire box in the sense that if the wall between the parts is removed the state of the system will change until it reaches a new equilibrium. By the same argument, if the removal of the partition results in no observable change of state we declare the two parts to be in equilibrium with each other and conclude that they both have the same temperature and pressure. For a multicomponent system we also require uniformity of the chemical potential of all components.

The partitioned system is an idealization of a gradient in temperature and pressure: while each part is individually in thermal and mechanical equilibrium, the overall system is not, because it is characterized by non-uniform temperature and pressure.

Answer 6

Whether you can or cannot specify a single temperature is not related to being reversible or not. There are inherently irreversible processes irrespective of its velocity, for example, the hysteretic behavior of a ferromagnet is always dissipative and thus irreversible at any rate of the process. Similarly, the plastic deformation of a metal bar is always dissipative and irreversible. And, of course, if these processes are done very slowly but in thermal contact (diabatic) with its environment then the temperature inside will be uniform and will be the same as that of the environment.

It is true though that if the process is not quasi-static then the local temperature variations may not have time equalize and there is no single temperature in the system and when it equalizes the local heat conduction results in in irreversible behavior. The two examples show a quasi-static process can be irreversible and thus quasi-static $\ne$ reversible, though it is sometimes the two are confused.

Your quote refers to a gas, but even there for an adiabatically isolated ideal gas can have isothermal irreversible process when it expands without work in an empty space. The workless expansion of ideal gas into a vacuum is isothermal, as Joule's experiment showed, but it is obviously irreversible.