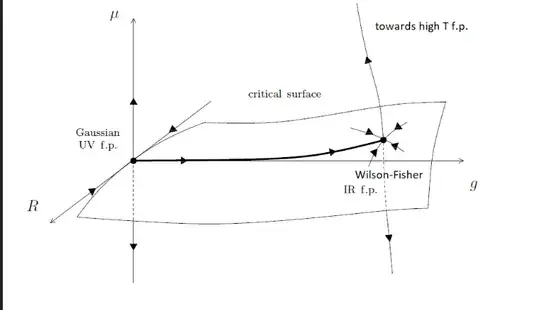
Given a $\phi^4$ theory in $d<4$ $$S_{\Lambda} = \int d^dx \left[\frac{1}{2}(\partial_i \phi)^2 + \frac{1}{2} \mu_0^2 \phi^2 + \Lambda^{d-4} \tilde{g}_0 \phi^4 \right]\,,$$ the corresponding RG flows in the coupling space are qualitatively like the ones shown in the picture. The question is whether the high Temperature fixed point, which corresponds to $\xi=0$, is unique. For example, do the vertical lines emanating from the Gaussian f.p. and the Wilson-Fisher f.p. both lead to a (high temperature) fixed point, and if so, do they meet at some point?
Asked
Active
Viewed 167 times