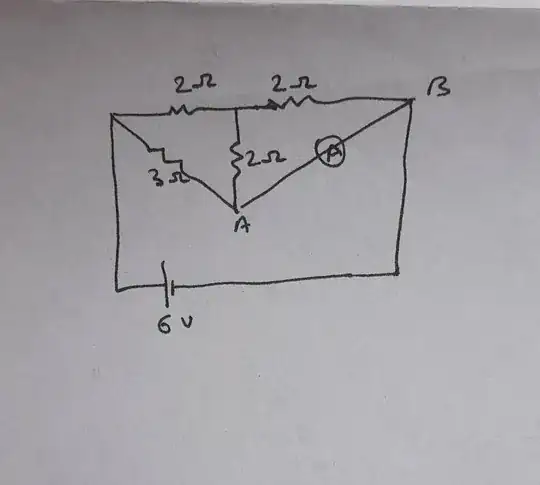
Shouldn't the ammeter between A and B read zero because A and B are maintained at the same potential, and for current to flow, a potential difference is required?
On the other hand, the current that entered the resistances has to return to the circuit through AB, which means that the ammeter's reading will be a non-zero value.
You are using Ohm's law in the form
$V_{AB}=I_{AB}R_{AB}$
to say that if $V_{AB}$ (the potential difference between A and B) is $0$ then $I_{AB}$ (the current flowing between A and B) is $0$. This would be true if $R_{AB}$ (the resistance between A and B) were not zero. But since $R_{AB}$ is $0$ we have
$0 = I_{AB} \times 0$
which is true for any value of $I_{AB}$ whatsoever. So you cannot use Ohm's law directly - you have to use it indirectly by finding the current through each of the other resistors in the circuit. Then add the currents through the two resistors that end at A to find $I_{AB}$.
As gandalf61 said, you have to go through every part of the wires instead of the whole thing. It is not because two point has the same potential that the path of the energy/electron has the same potential everywhere.
In general relativity, an electron wouldn't see the same potential at both point I believe.
Correct me if wrong, I'm here to learn as well. Cheers
