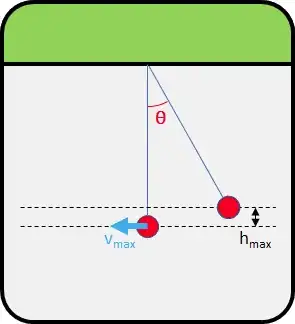
I have done the following work. Consider the following pendulum and measurements:
Assume the length of the pendulum is $r$. Then the following calculations can be done:
$h_{max} = r - r\cos{\theta}$
$U_g = mgh_{max} = mg(r-r\cos{\theta}) = \frac{1}{2}mv^2 = KE \implies v_{max} = \sqrt{2g(r-r\cos{\theta})}$
We are solving for the period length, $T$. Consider the velocity vs. time graph of this pendulum. It will have the following equation: $v(t) = v_{max}\sin{\frac{\pi t}{T}}$ (I got this by letting one period of the sin graph be $2T$, since one swing of the pendulum is half of the graph's period). It is known that the area under a velocity vs. time graph is equal to displacement, which, in this case, is $2r\sin{\theta}$. Therefore, we solve the following equation for $T$, giving us our answer:
$$\int_0^T v(t)dt = 2r\sin{\theta}.$$
Did I make a mistake in my reasoning? When I solve for $T$, I get $\frac{\pi}{2} \sqrt{\frac{r}{g}} \left( \frac{\sin{\theta}}{\sin{\frac{\theta}{2}}} \right)$, which is not correct. Thank you in advance.