Addition of forces on a rigid body instead of a point

Question

When two forces act on a point mass,we add the forces like we usually do and i have no problem understanding that. When the same forces are applied on a rigid body,how are we able to add them the same way?

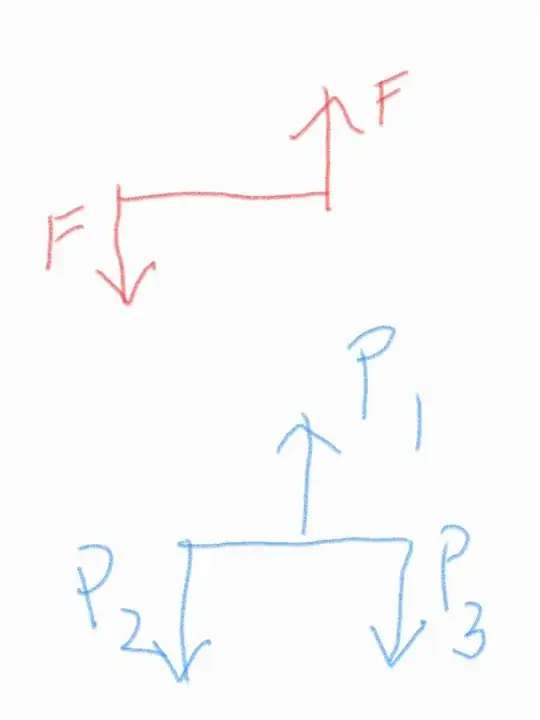
1. In the first diagram,what we have is a couple. And almost everywhere it is said that it can only produce rotational motion and no translational motion since opposite forces cancel out. But don't we cancel out opposite forces if they acted on the same particle? What is the proof that we can cancel out forces like this when the scenario is extended to a bigger body? So when doing $F+(-F)=0$ aren't we considering that bigger body as a point particle? I just wanted to know why it is justified to treat the bigger body as a point particle in terms of adding forces.

2)The second diagram is also the same thing. Typically when we say that the extended body is in equilibrium, we at first add the downward forces in $-y$ axis $P_2+P_3$ just as if the bigger body was a point particle,meaning both the forces $P_2$ and $P_3$ are acting at the same point mass. Then we say for equilibrium we need $P_1=P_2+P_3$. I would have no problem admitting these only if it were a point particle instead of an extended body. But i am finding it hard to digest why we can treat the extended body like a point mass while adding forces.

So my main dilemma is to find a proof why we can treat extended objects as if they were point particles while adding forces and also what is the proof that the whole body will experience the same linear effect due to the force which is actually applied at only one certain point of the body.

Answer 1

Extended objects, or in general any mass configuration, do obey Newton's second law. You don't have to assume you can treat the system just like a point mass, you can formally treat it as a collection of point masses and show that it obeys the same law.

Suppose you have a system that is a collection of masses $m_i$. $m_i$ applies an internal force on $m_j$, which we will denote by $\vec F^\text{int}_{ij}$, "int" standing for internal. An example of internal forces is the elastic forces keeping a rigid body "rigid". In addition to the internal forces, on each mass $m_i$ is an external force $\vec F^\text{ext}_{i}$

Newton's second law applied to mass $m_i$ says $$\vec F^\text{ext}_{i}+\sum_{j\ne i}\vec F^\text{int}_{ji}=\frac{d\vec p_i}{dt}.$$ Adding these for all $i$, $$\vec F^\text{ext}+\sum_{i}\sum_{j\ne i}\vec F^\text{int}_{ji}=\frac{d\vec P}{dt}$$ where $\vec F^\text{ext}=\sum\limits_i\vec F_i^\text{ext}$ is the sum of the external forces on the system and $\vec P=\sum\limits_i\vec p_i$ is the total momentum of the system. We will now deal with the double sum of internal forces. We can write $$\sum_{i}\sum_{j\ne i}\vec F^\text{int}_{ji}=\sum_{i}\left(\sum_{j< i}\vec F^\text{int}_{ji}+\sum_{j> i}\vec F^\text{int}_{ji}\right)$$ $$=\sum_{i}\sum_{j< i}\vec F^\text{int}_{ji}+\sum_{i}\sum_{j> i}\vec F^\text{int}_{ji}$$ $$=\sum_{i}\sum_{j< i}\vec F^\text{int}_{ji}+\sum_{j}\sum_{i< j}\vec F^\text{int}_{ji}$$ $$=\sum_{i}\sum_{j< i}\vec F^\text{int}_{ji}+\sum_{i}\sum_{j<i}\vec F^\text{int}_{ij}$$ $$=\sum_{i}\sum_{j< i}\left(\vec F^\text{int}_{ji}+\vec F^\text{int}_{ij}\right).$$

This is just a way of formally showing that for each $m_i$ applying a force on $m_j$, there is a force $m_j$ applies back on $m_i$. By Newton's third law, these are equal in magnitude and opposite in direction, i.e. $\vec F^\text{int}_{ij} = -\vec F^\text{int}_{ji}$, so the double sum is zero, and $$\vec F^\text{ext}=\frac{d\vec P}{dt}.$$

Answer 2

We can perform the vector sum of external forces to get net external force $\overrightarrow F_{ext}$ on any object not just a point mass or a rigid body but any collection particles interacting or non interacting. $\overrightarrow F = m\overrightarrow a$ so a force produces an acceleration, in case of point mass it is clear that this acceleration is of the point mass itself, but what about a non point mass body? How will you define the acceleration of that body? It might be possible in some cases that all the points in the body have same acceleration, but in general it might not be true. For example in the your first diagram the object is rotating hence different points have different acceleration depending on its distance from the center of the rod.

For non-point mass bodies, $\overrightarrow F_{net} = M_{total}\overrightarrow a_{com}$ where $a_{com}$ is the acceleration of the Center of Mass of the body. Where the position vector of the Centre of Mass of the Body $B$ is defined as, $\overrightarrow r_{com} = \frac{1}{M_{total}}\iiint_B \rho(\overrightarrow r)\overrightarrow r dV$. Where $\rho(\overrightarrow r)$ is the mass density at position $\overrightarrow r$.

Twice differentiating it with respect to time gives $\overrightarrow a_{com} = \frac{1}{M_{total}}\iiint_B \rho(\overrightarrow r)\frac{d^2\overrightarrow r}{dt^2} dV$, where you can think $\frac{d^2\overrightarrow r}{dt^2}$ as the acceleration of small mass region of body at $\overrightarrow r$.

Now it can be proved that the net external force on any kind of body is the vector sum of all external forces, that is $\overrightarrow F_{net} = \Sigma \overrightarrow F_{ext}$

Proof:

Consider the small volume element $dV$ of the body. Its mass will be $dm = \rho(\overrightarrow r)dV$. for this element, $\overrightarrow F_{int} + \overrightarrow F_{ext} = dm\frac{d^2\overrightarrow r}{dt^2}$, where $\overrightarrow F_{int}$ is the net internal force, the force on this element by the rest of the body, and $\overrightarrow F_{ext}$ is the net external force(forces other than that applied by the rest of the body) on this element.

Performing a vector sum over entire body B we get,

$\Sigma \overrightarrow F_{ext} +\Sigma_B \overrightarrow F_{int} = M_{total}.\frac{1}{M_{total}}\iiint_B \rho(\overrightarrow r)\frac{d^2\overrightarrow r}{dt^2} dV = M_{total}.\overrightarrow a_{com}$

It can be shown that $\Sigma_B \overrightarrow F_{int} = 0$

so, $\Sigma \overrightarrow F_{ext} = M_{total}.\overrightarrow a_{com} = \overrightarrow F_{net}$ hence we have shown that the net force on any body is the vector sum of all the external forces.

In the couple the net external force $=\Sigma \overrightarrow F_{ext} = 0$ which implies that $a_{com} = 0$ which is true as the centre of mass for a rod is at its center and has zero acceleration, but other points in the body do have non-zero acceleration.

Answer 3

what is the proof that the whole body will experience the same linear effect due to the force which is actually applied at only one certain point of the body.

There is NO proof. This is in fact a definition of rigid bodies in classical mechanics.

Such distribution of forces on body particles even if it happens to act at a single point is not necessarily true for all objects. Some objects in universe do so and some do not , and the ones who do it are called as "rigid bodies" by human beings, which are heavily studied in your educational courses.

Answer 4

For a system of particles, assuming Newton's third law is valid, it can be shown that $\sum \vec F^{\space ext} = M \vec a_{CM}$ where $\sum \vec F^{\space ext}$ is the vector sum of all the external forces, $M$ the total mass, and $\vec a_{CM}$ the acceleration of the center of mass (CM). For the proof, see the textbooks Mechanics, by Symon or Classical Mechanics, by Goldstein. If the third law is valid the internal forces do not contribute to the motion of the CM. There are certain forces (e.g., electromagnetic) for which the third law is not valid. But, for traditional cases in classical mechanics the third law is valid.

This result is valid for a system of particles, a rigid body being a special case.