I am confused about all these different interpretations of what a photon is?
I am looking for a simple and practical interpretation.
Therefore, I am asking herein if a single photon corresponds to a single period $T$ and wavelength $λ$ of the sinosoidal wave function of a poynting vector of monochromatic light?
image credits: https://www.tutorialspoint.com/antenna_theory/antenna_theory_poynting_vector.htm
A photon, as with any quantum system, is described by its wave function. So when you're asking what a photon looks like this is equivalent to asking what the wave function of a photon looks like.
Now what exactly we mean by the wave function of a photon is a little involved (see EM wave function & photon wavefunction for more on this) but for most purposes we can take the photon to be just the EM wave that we get from solving Maxwell's equations. So the wave function of the photon is just an EM wave suitably normalised. Then your diagram could be showing (part of) the wavefunction of a single photon.
To complicate matters further, quantum particles are always delocalised to some extent. That means they are more like a fuzzy cloud that extends over some region of space rather than the little ball as we might naively picture a particle. Typically the particle would be described as a wave packet:
(picture from the Wikipedia link above)
where the width of the wave packet gives the distance over which the particle is delocalised.
Incidentally this is what John Doty means by:
A single gamma ray photon from technetium-99m represents an electromagnetic wave train of $\approx 10^{24}$ cycles!
i.e. the photons emitted by technetium-99m decay are delocalised over a distance approximately equal to $10^{24}$ times their wavelength.
So your diagram:
would represent a photon wave packet with a size equal to three wavelengths. It's not a question of where in the picture do we find a photon - the whole picture is the photon.
The next question is where are the individual photons in a light wave, and again this is involved because a light wave, or more precisely a coherent state of photons, does not have a precisely defined number of photons in it. However for most purposes we can take the EM wave of the light to be simple the sum of the EM waves for all the photons in it.
If the photon represents monochromatic light, it is not localized until detected, so you cannot relate it to your diagram the way you wish. In real life, there is no perfectly monochromatic radiation. A single cycle is far from monochromatic: it consists of a broad band of frequencies (energies). Longer sinusoidal wave trains have narrower bandwidths, so they are closer to monochromatic.
A single gamma ray photon from technetium-99m represents an electromagnetic wave train of $\approx 10^{24}$ cycles! It only "collapses" to a specific time of photon emission when it interacts irreversibly with a detector or other object.
A quick inverse answer to the question: Is a photon a single period of a sine wave?
No.
But: A coherent classical plane wave has a description in terms of Fock state (photon number states). This is in the quantum optics Hamiltonian formulation of light, which is quite different from the relativistic Lagrangian formulation (QED).
It's called the Glauber state (https://en.wikipedia.org/wiki/Coherent_state). It's a sum over an infinte number of photon states such that is an eigenstate of annihilation operator.
From there: Express a single period of sine in terms of plane waves (basic Fourier transformation), and the plug those into the coherent state, and see what the Fock space state look like.
It will be an exercise in exponentials and $a$, $a^{\dagger}$.
In quantum physics, every item has both wave and particle qualities. Nothing is exclusively a traditional particle or a traditional wave. Each item has frequency and wavelength. Each has energy and momentum. Each has spin (often measured as angular momentum), although some have spin zero. A photon actually has spin 1. You cannot measure everything all at once. Measuring some quantities will change others. Some items combine such that the particle qualities usually stand out more. Some combine such that the wave properties are more visible. Mass seems to affect this (although the definition of mass is currently under debate). An EM wave striking a metal surface and knocking electrons off is an example of the particle-like properties of photons standing out. A different frequency changes the kinetic energy of individual electrons. Changing the intensity of the light only increases the number of electrons, not their individual energies. One photon strikes loose one electron. On the other hand, things such as diffraction, refraction, and interference emphasize the wave properties of photons. "Wave packet" is a popular term for these wave/particle items. We know how to measure them and use them, but we don't really know what they are.
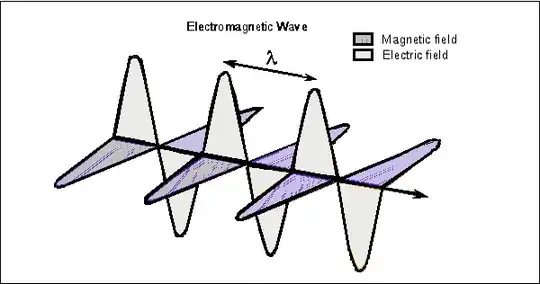
From an Electromagnetic Theory classical standpoint and energy-wise description, form my experience, educationally it is perfectly fine to equalize a single photon with one wavelength period of a Poynting vector of monochromatic light, during its propagation in space.
Since the energy of a single photon is equal with the energy of a single wavelength of monochromatic light consisting from these photons according to the general expression:
$$E_{Ph}=E_{wl}=hc/λ.$$
where $h$, $c$ and $λ$ are the Planck constant , the speed of light in free space and the wavelength of light accordingly.
Notice, the Poynting vector illustration shown in the question's figure could represent a beam of monochromatic light with the photoemitter calibrated to output sequentially an ideally one photon each time. Of course if there are more than one photons output each time then they would stack together and increase the intensity of the beam (i.e. amplitude in the poynting vector shown). But yes, the figure shown assumes one photon is transmitted each time in sequence on the poynting vector.
Sine wave function is 100% compatible with the spin 1 thus 2π-symmetry characteristic of a normal photon. Energy-wise, with the assumption that the amplitude shown in the Poynting vector wave illustration herein corresponds to a single photon each time present in the photon train, the illustration is correct. Surely as an isolated particle the photon is not a sine wave rather a standing wave however its interaction with its environment when propagating through space is as an electromagnetic sine wave. The later is exactly what this Poynting vector is showing.
Also, to complete the above Poynting vector educational representation of a single photon of monochromatic light propagating through space with $c$ speed and say of angular frequency $ω$ in rad/s shown in the question's figure above, we must be able to calculate the Poynting vector amplitude (i.e. intensity of single photon of monochromatic light of a given frequency).
"The magnitude of amplitude of the Poynting vector (energy flow) of the photon is:
$$ \mathscr{P}_0=\varepsilon_0 c E_0^2=\hbar \omega^4 / 4 \pi \alpha c^2 $$
Where, $\hbar$ is the reduced Planck Constant and $α$ the Fine Structure Constant" [1].
