0

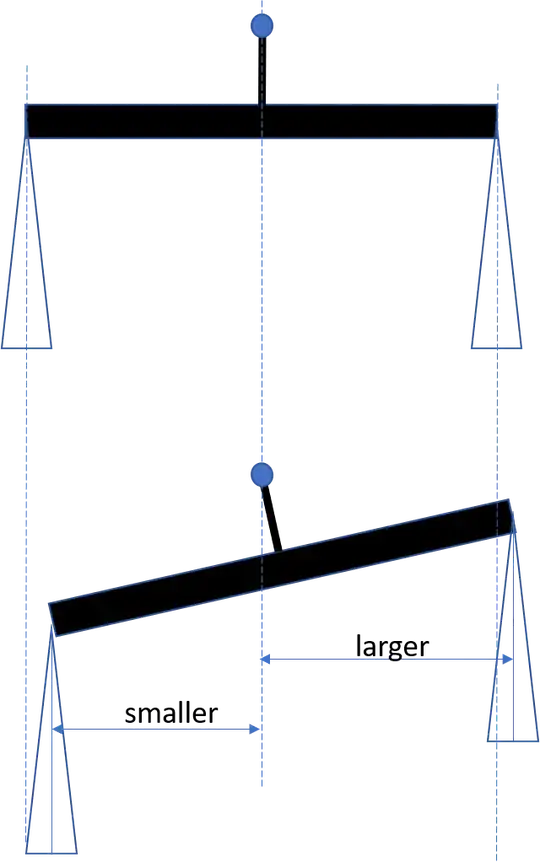
This question was previously asked 11 years ago here, but I believe it does not answer my question for the following reasons:

(A) The first answer takes a different system, mine looks like this.

(B) The second answer says that tangential torques are different but doesn't explain why, which is my question. The tangential torques are both $mg\sinθr$, where $r$ is the distance of the weights from the pivot and $θ$ is the angle of deflection with the horizontal. The centre of mass is also vertically below the pivot as no force is applied in the horizontal direction.

Gert
  • 35,561
CallousCalculus
  • 71

2 Answers2

2

balance beam diagram

Torque about a given axis equals force times distance of line of action of the force from the given axis.

Andrew Steane
  • 65,285
1

The centre of mass of the system, beam and scale pans, is below the pivot point and when the beam is displaced from the horizontal the centre of mass moves to one side of the pivot.
The system then moves towards the position of stable equilibrium under the influence of the restoring torque produced by the centre of mass.

For the type of balance shown in the video remove the scale pans.

enter image description here

You might find it difficult to get the beam to balance horizontally as the pivot is roughly coincident with the position of the centre of mass of the beam.

Now make a new hole in the beam "above" the central hole .
Try to get the beam to balance when the beam is pivoted at the new hole when the new hole is below the old hole, and then when the new hole is above the old hole.
In one position it will be a position of unstable equilibrium, new hole below old hole, and move towards the other position which is one of stable equilibrium, new hole above centre of mass.

Farcher
  • 104,498