Charge distribution on a system of 3 capacitors when the middle one is earthed

Question

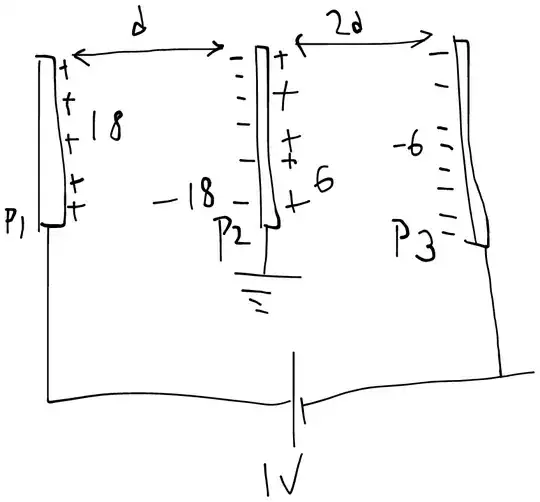
Three conducting sheets 1,2 and 3 are placed parallel to each other such that separation between them is negligible. Sheet 1 and sheet 3 are given charges $+Q$ and $+3Q$ respectively. $Q=3 \space mC$ and $\epsilon_0A/d=30 \space mF$

Case 1: Suppose plate 2 is now earthed. Give the charge distribution on the three capacitor plates.

Case 2: Now a battery of EMF $1 \space V$ is connected across plates 1 and 3. What would be the charge distribution now?

---

Case 2 is pretty straightforward. Since the faces are connected by a wire, the outer faces of plate 1 and 3 cannot have any charge on them. So we just assume that plate 1 as some charge $Q+q$ and plate 3's inner plate has some charge $3Q-q$. Using kirchoff's voltage law trivially gives $q=15 \space mC$. It did not matter if the middle plate was earthed or not. The charge distribution is as follows:

Case 1 is where I am having a lot of trouble. First I considered that since the area between inner plates 1 and 2 and area between inner plates 2 and 3 is electrostatically shielded and since the charges on the outer faces of 1 and 3 will always have same charge, they must have same potential (they have same charge so by symmetry) and if they did, then it would be simple parallel configuration of capacitors, but this argument quickly falls apart when one considers the case when 2 is not earthed. When 2 is not earthed the charge configuration looks something like this,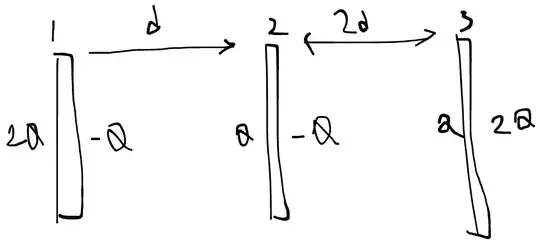 where obviously plates 1 and 3 are not at same potential. What is wrong in my reasoning? What does it mean to earth a capacitor? Is it $V=0$? If not, how else can I mathematically depict earthing something?

Answer 1

It may help to take a slightly more kinematical view, different brains just kind of work differently and it looks like you might want a better sense of the mechanisms involved and the little motions of electrons and stuff, so I wanted to provide that answer.

To Earth the capacitor on this view, is to connect it with a wire to “infinity,” beyond where the sheets look like sheets. What I mean is that, if you are off at infinity looking at this capacitor, it appears to have all the properties of a point charge with charge 4Q, you are so far away that the spatial distribution is negligible and indeed you are so far away that the $-4Q/r$ potential is no longer substantially different from zero, too.

If you let charge flow off to infinity in this case, it will keep moving until when? Until that observer at infinity thinks the system is electrically neutral: because if it all collapses into a net point charge anyway, that point charge is going to be pulling electrons down the wire unless its net charge is 0.

So, earthing leads to +Q, -4Q, +3Q, overall charge is zero, and you basically have two capacitors in parallel. Let's see how the charge distributes among the various boundaries.

Switching back to the regime where you pretend the sheets are large or infinite and ignore what is happening at the edges, infinite sheets of charge have a force law that does not diminish with distance, and so for a very different reason than before, a test charge outside of the capacitor sees a force from all the charge sheets of the capacitor as if they came together from one single wall of net charge. But that net charge is now zero! So, the force on the test charge outside the capacitor is zero.

Then we consider a test charge inside the first conductor, it also needs to experience zero force inside the metal simply because it is a good conductor, if there was any E-field inside of it, it would have moved to the electrons to compensate... Wait, that is exactly the same as the charge outside, so we do not need any charge on the outside surfaces of the capacitor to explain the discrepancy! The first Maxwell equation says that the charge density explains discontinuities in the electric field lines, but the field lines on both sides are zero: no discontinuity, therefore no charge.

This puts the full charge +Q on the inner surface of that conductor, and a symmetrical argument puts the other charge +3Q on the inner surface of its conductor.

Inside the middle conductor, you again use the fact that the electric field must be zero inside of a conductor, otherwise the charge would be moving around. Seeing a wall of +Q pushing from one way and +3Q pushing from the other, the net electric field would be like a wall of +2Q where the 3Q wall is, if that makes sense. So the surfaces of the middle conductor with charges $q_{1,2}$ need a discrepancy of $q_1-q_2= 2Q$ between their charges to compensate and leave zero field inside the conductor. You also know that $q_1+q_2 ={-4Q},$ very simple system of equations, solve away, the answer looks nice and symmetric.

Answer 2

Original not-quite-right answer:

Nothing is wrong with your reasoning. What it means to ground (earth) a conductor depends on how you're thinking about it. From a potential point of view, grounding means defining its potential to be zero (so the other plates have potentials that are not zero in this case). From a charge point of view, grounding means connecting it to a source that can give or take an unlimited amount of charge. If plate 2 is isolated (not grounded), then its two faces must have equal and opposite charge. But if it is grounded, charge is free to flow in from ground, or out to ground. Your picture shows that in this case a net 12 mC of charge flows from the plate to ground.

Better answer: In Part 1, charge flows from ground until the surfaces of plate 2 have equal and opposite charge to their respective opposing plates, that is, $-Q$ on the left and $-3Q$ on the right. You can prove this by applying Gauss's Law to a box with one end interior to in the material of the middle plate and the other end interior to in the material of an outer plate. $E=0$ at both ends of the box (inside a conductor at equilibrium) and so the net charge inside the box must be zero.

[Edit: changed "interior to" to "in the material of" for clarity.]

In Part 2 I think we must assume the middle plate remains grounded. Now the battery moves charge around until the potential difference between the outer plates reaches one volt. Symmetry dictates that the middle plate has a potential halfway between that of the two outer plates (in fact it's defined to be zero by grounding, so the outer plates are at $\pm 0.5$ volts). Note that because plate 2 is grounded, the charge on each side of plate 2 will adjust to be equal and opposite to the outer plate charges. You've been given the capacitance $C\equiv\epsilon_0A/d$, so you can use $Q=CV$ to find the $Q$'s.