Does every photon have same momentum because they have same velocity $= c =3\times 10^{8}$ m/s?

Question

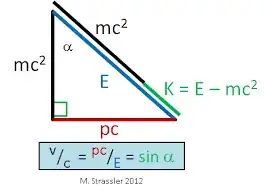
I am new to Stack Exchange as well as physics.

Momentum is $$p={\rm mass} \times {\rm velocity}=mv.$$ So, if a photon has rest mass $m=0$, [Also what is "rest" mass?], and $v$ is always $c$, then $p$ is always constant.

We know kinetic energy is $$E = \frac{1}{2}mv^{2}= \frac{(mv)^{2}}{2m}= \frac{p^{2}}{2m}.$$
$E$ is proportional to $p^{2}$, so if $p$ is constant, $E$ is also constant from photon to photon. However, $$\lambda = \frac{h}{mc}= \frac{h}{p},$$ where $h$ is Planck's constant. Hence, we get that $p$ is inversely proportional to $\lambda$ (wavelength).

So light waves with lower wavelength or higher frequency have more momentum and hence, more kinetic energy. Overall I am confused by these contradictory conclusions.

Answer 1

The equations you cited are non-relativistic approximations. When dealing with light or other fast objects they do not work. The key equation relating mass energy and momentum for all systems is $$m^2 c^2=E^2/c^2-p^2$$The $m$ in this equation is the “invariant mass”, which is what mainstream physicists refer to when they say the word “mass” without qualification. ("Rest mass" is an older name for the same quantity.) This is the mass that is an intrinsic property of the object, and not a reflection of the observer.

Specifically, when a photon is described as massless it is the invariant mass that is 0. Putting $m=0$ into the equation immediately gives $p=E/c$, so a photon with more energy will have more momentum.

To get velocities we can also use $$v=\frac{c^2 p}{E}$$ This formula is relativistic also, so it works for fast moving objects. For something massless we showed that $p=E/c$ so now we easily obtain $v=c$. Thus anything massless will travel at $c$.

In summary, a massless object, like a photon, has momentum that is directly proportional to its energy, but always travels at $c$.

Answer 2

All particles and objects, massless or not, satisfy $$ E^2 = (pc)^2 + (mc^2)^2 ,$$ where $E$ is the total energy, While kinetic energy ($T$) satisfies $$ E = T + mc^2. $$ Note that if $p \ll mc $: $$ T = \left[(pc)^2 + (mc^2)^2 \right]^{\frac 1 2} - mc^2 $$ $$ T = mc^2\left(\frac{p^2}{m^2c^2} + 1 \right)^{\frac 1 2} -mc^2$$ $$ T \approx mc^2\left(1 + \frac 1 2\frac{p^2}{m^2c^2}\right) - mc^2 = \frac{p^2}{2m} = \frac 1 2 mv^2,$$ recovering the Newtonian equation.

The general result is often shown as a right triangle, with hypotenuse $mc^2 +T$ ($T\equiv K$ in the figure).

In terms of the de Broglie relation, it's clearer to use the wave vector, $$ \left|\left|\vec k \right|\right| = \frac{2\pi}{\lambda},$$ so $$ \vec p = \hbar \vec k $$ $$ E = \hbar \omega, $$ which can be combined into Lorentz covariant 4-vectors: $$ p^{\mu} = (E/c, \vec p) = \hbar k^{\mu} = \hbar\left(\omega/c, \vec k\right). $$

In the rest frame of a particle (which photons don't have), $$\left(\frac{mc^2}{c} , 0,0,0\right) = \hbar(\omega_0/c, 0, 0, 0), $$ with $$ \omega_0 = \frac{mc^2}{\hbar} ,$$ so mass appears as a cutoff frequency at zero wave-number (momentum), as seen in waveguides. In my opinion, this is a better way to think of the Higgs field as "giving mass" than the usual, "It's like molasses," (which so not Lorentz invariant).

Answer 3

This is most easily understood by using the unfashionable $E=mc^2$. Some will tell you this is "wrong", but it merely represents a different model of what mass is than is currently fashionable in mathematical physics. Then, $m=E/c^2$, and $p=mv=mc$ tells you that photon momentum is proportional to energy.

And, of course, this answer will be voted down by those who prefer the obfuscation that results from modeling the photon as massless.