Geodesics: Energy functional vs length functional

Question

The Wikipedia article about geodesics talks about the equivalence of obtaining the geodesic by either minimizing the length functional $L$, or by minimizing the energy functional $L^2/2$, cf. the Phys.SE post Geodesic Equation from variation: Is the squared lagrangian equivalent?

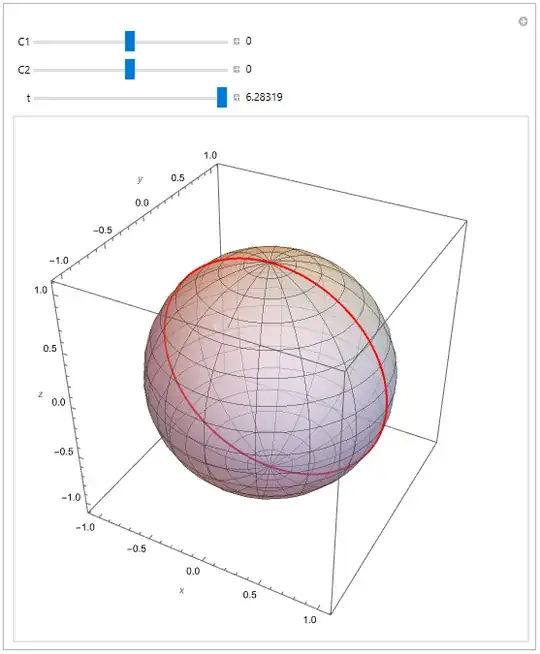
In my courses so far, I haven't heard about the latter technique, so I was curious to see whether both approaches yield the same geodesic. I chose the geodesics on the unit sphere because it has the well-known solution of great circles.

Minimizing the length functional:

Given the spherical symmetry of the problem, start with the line element in spherical coordinates:

\begin{equation} ds^2=dr^2+r^2d\theta^2+r^2\sin^2\theta\,d\varphi^2 \end{equation}

For $r=1$ and factoring out $d\theta$, we get the arc length as the integral over $ds$: \begin{equation} l=\int ds=\int\limits_{\theta_1}^{\theta_2}\underbrace{\sqrt{1+\sin^2\theta\,\varphi'(\theta)^2}}_{\displaystyle L}\,d\theta \end{equation}

Then, plug in the Lagrangian $L$ in the Euler-Lagrange equation \begin{equation} \frac{\partial L}{\partial \varphi}-\frac{d}{d\theta}\frac{\partial L}{\partial \varphi'}=0 \end{equation}

until we arrive at $\displaystyle\varphi(\theta)=\int\frac{C_1}{\sin\theta\sqrt{\sin^2\theta-C_1^2}}\,d\theta$ . This result can be simplified using eq. (16) to yield

\begin{equation} \varphi(\theta)=-\arcsin\left(\frac{C_1\cot(\theta)}{\sqrt{1-C_1^2}}\right)+C_2 \end{equation}

which, as far as I understand, is the necessary condition for the curve to be a geodesic on the sphere. Insert into the parametrization of the unit sphere: \begin{equation} \theta\mapsto\begin{pmatrix} \sin\theta\cos\varphi(\theta) \\ \sin\theta\sin\varphi(\theta) \\ \cos\theta \end{pmatrix} \end{equation}

Mathematica produces the following plot:

                                  

Minimizing the energy functional:

Perform the same calculation as above using the squared Lagrangian, multiplied by $1/2$: \begin{equation} L^*=\frac{L^2}{2}=\frac{1}{2}\left(1+\sin^2\theta\,\varphi'(\theta)^2\right) \end{equation}

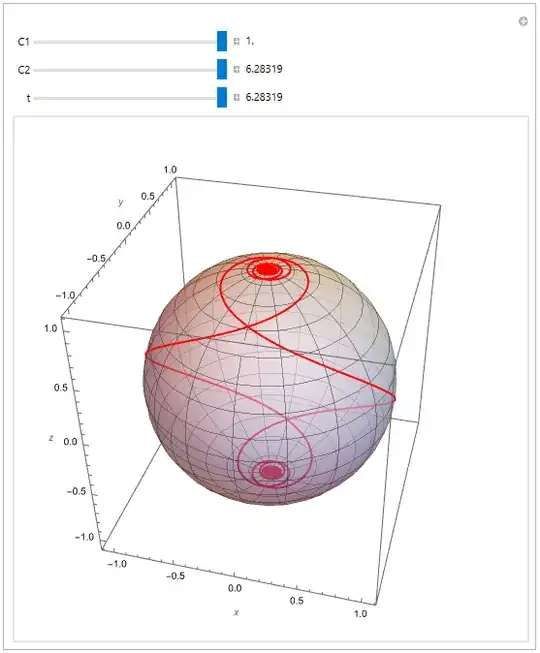
The E-L equation yields \begin{equation} \varphi(\theta)=\int \frac{C_1}{\sin^2\theta}\,d\theta=-C_1\cot(\theta)+C_2 \end{equation}

This time, the resulting curve does not look like a great circle whenever $C_1\neq 0$. What did I miss?

                                  

---

Mathematica code for the first plot:

\[CurlyPhi][\[Theta]_, C1_, C2_] := -ArcSin[(C1 Cot[\[Theta]])/Sqrt[1 - C1^2]] + C2
Manipulate[Show[ParametricPlot3D[sphere[{\[Theta], \[CurlyPhi]}], {\[Theta], 0, \[Pi]}, {\[CurlyPhi], 0, 2 \[Pi]}, PlotStyle -> {White, Opacity[0.6]}, ImageSize -> 500, AxesLabel -> {x, y, z}], ParametricPlot3D[{Sin[\[Theta]] Cos[\[CurlyPhi][\[Theta], C1, C2]], Sin[\[Theta]] Sin[\[CurlyPhi][\[Theta], C1, C2]], Cos[\[Theta]]}, {\[Theta], 0, t}, PlotStyle -> Red, PlotPoints -> 100, MaxRecursion -> 5]], {{C1, 0}, -1, 1, Appearance -> "Labeled"}, {{C2, 0}, -2 \[Pi], 2 \[Pi], Appearance -> "Labeled"}, {{t, \[Pi]/2}, 0, 2 \[Pi], Appearance -> "Labeled"}]

Answer 1

You are using the wrong Lagrangian. You have two degrees of freedom $\theta,\phi$ and you need an additional “time” parameter to parametrize your trajectories. I’ll denote it $t$ so you are looking for equations of motion of $\theta(t),\phi(t)$.

These are given by two possible Lagrangians: $$ L=\frac{1}{2}(\dot\theta^2+\sin^2\theta\dot\phi^2) $$ Or $L’=\sqrt{2L}$.

In the first case, you have the equations of motion derived by Euler-Lagrange: \begin{align} \frac{d}{dt}\dot\theta-\sin\theta\cos\theta\dot\phi^2&=0 \\ \frac{d}{dt}(\sin^2\theta\dot\phi )&= 0 \end{align} In the second case, the equations of motion are: \begin{align} \frac{d}{dt}\frac{d\theta}{ds}-\sin\theta\cos\theta \frac{d\phi}{ds}^2&=0 \\ \frac{d}{dt}\left(\sin^2\theta \frac{d\phi}{ds}\right) &= 0 \end{align} with: $$ \frac{d}{ds}=\frac{1}{L’}\frac{d}{dt} $$

In either case, the curves will trace out great circles.

It is only in the second case that you have the curves are invariant by reparametrization (a case of gauge invariance). This is why you could remive a degree of freedom and parametrize the curve by $\theta$. However this is not true in the second case. The parametrization is fixed (it’s the arclength) and reparametrizing does not give you the same curves as you’ve observed.

In fact this is how you can go from $L’$ to $L$. You can lift gauge invariance by choosing the arclength as the parameter, adding an additional constraint.

Hope this helps.

Answer to comment

The usual method for solving such systems is by noticing that you have enough conservation laws for the system to be integrable. You have naturally two conserved quantities from direct inspection: $$ E=\frac{1}{2}(\dot\theta^2+\sin^2\theta\dot\phi^2) \\ L_z=\sin^2\theta\dot\phi $$ Actually, your system is superintegrable since you also have the other components of angular momentum that are also conserved.

You can use them to get a first order ODE in $\theta$ only: $$ \dot\theta=\sqrt{2E-\frac{L_z^2}{\sin^2\theta}} $$ You need only calculate the antiderivative of the inverse of the RHS. This can be done analytically using the change of variables to $z=\cos\theta$ and using the $\arccos$.

If you only wanted an equation of $\phi(\theta)$ as before, you could also manipulate the equations to get: $$ \frac{d\phi}{d\theta}=\frac{L_z}{\sin\theta\sqrt{2E\sin^2\theta-L_z^2}} $$ which can be integrated in a similar fashion.